Stress Waves Propagation in Layered Graded CellularMaterials under Dynamic Crush Loading
-
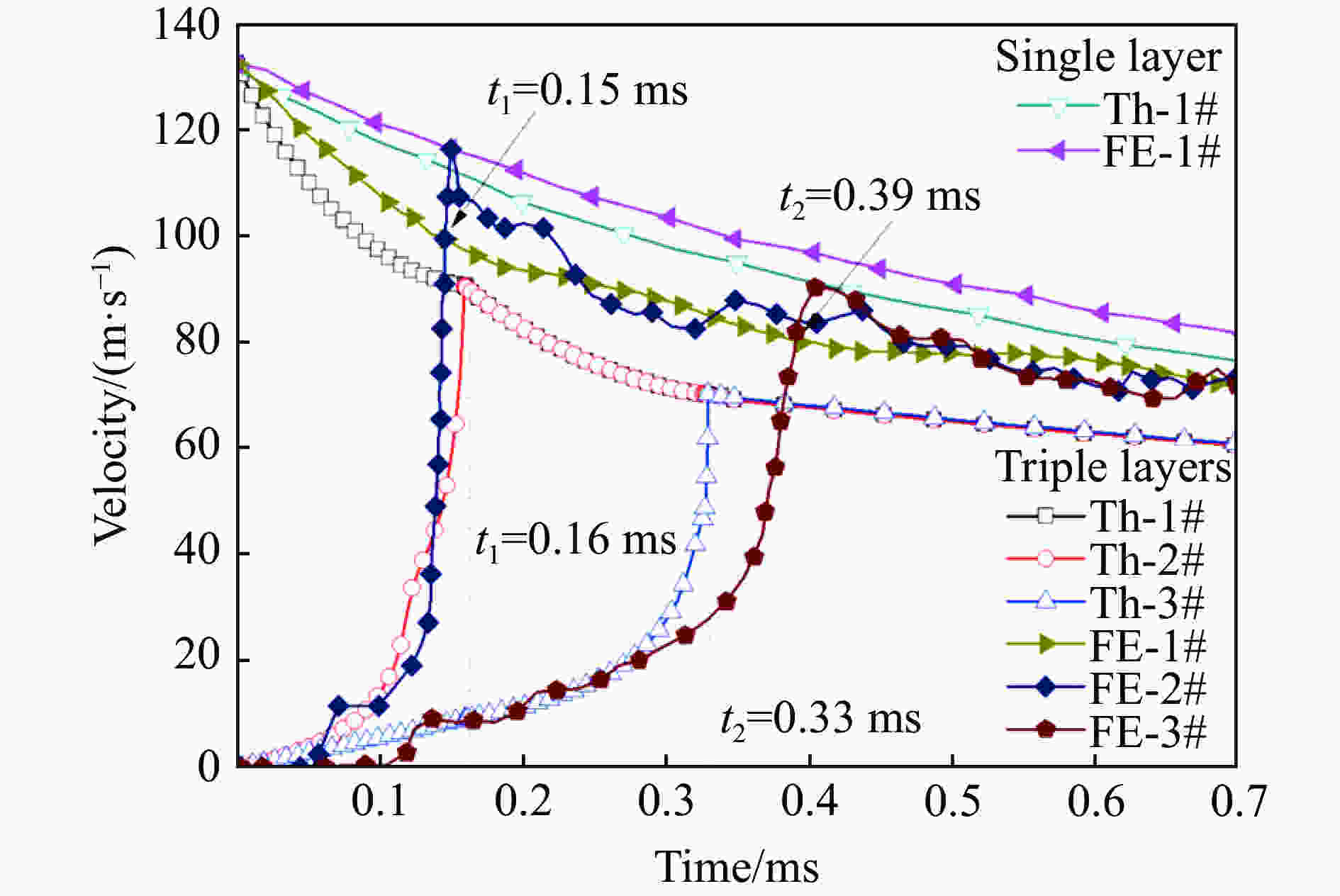
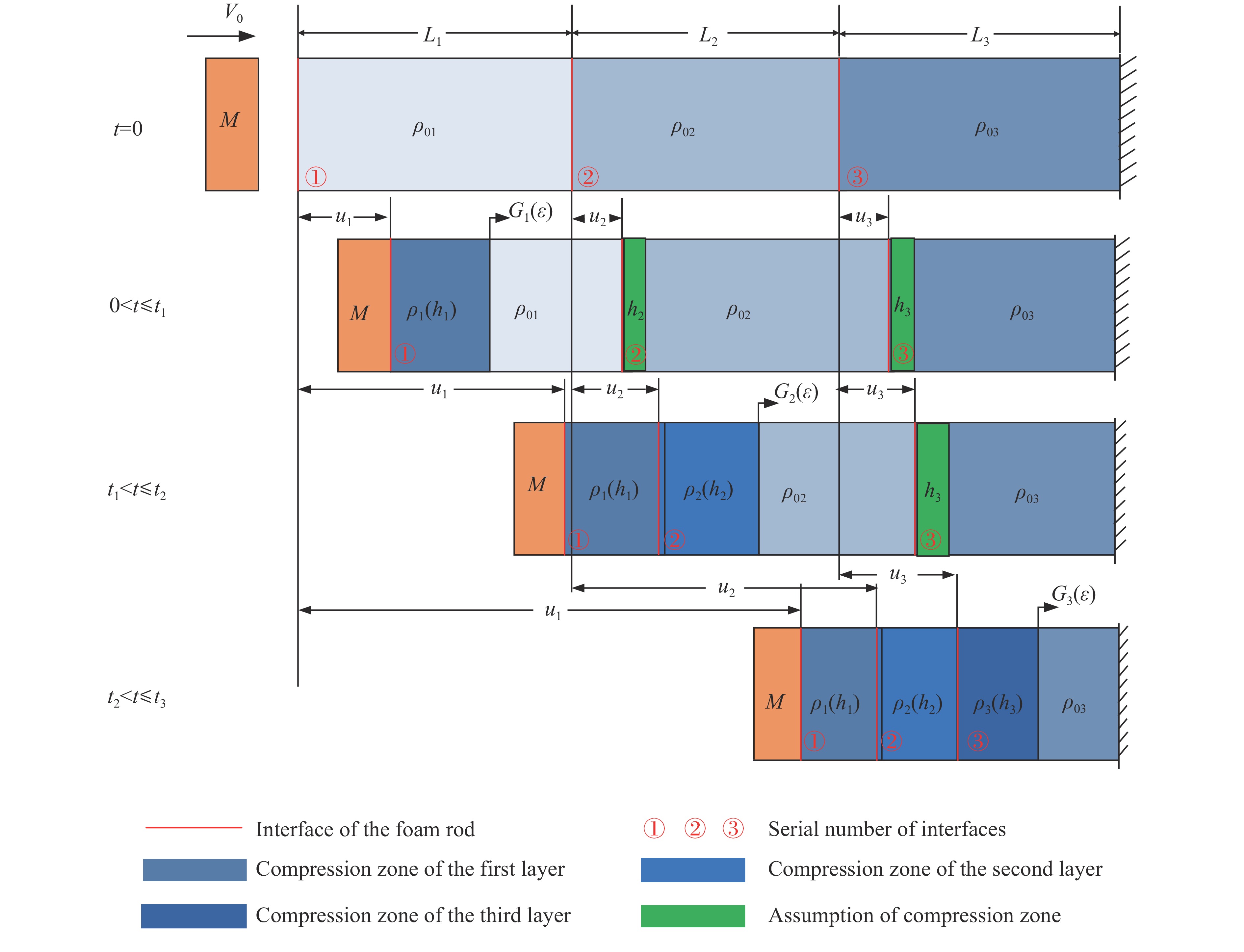
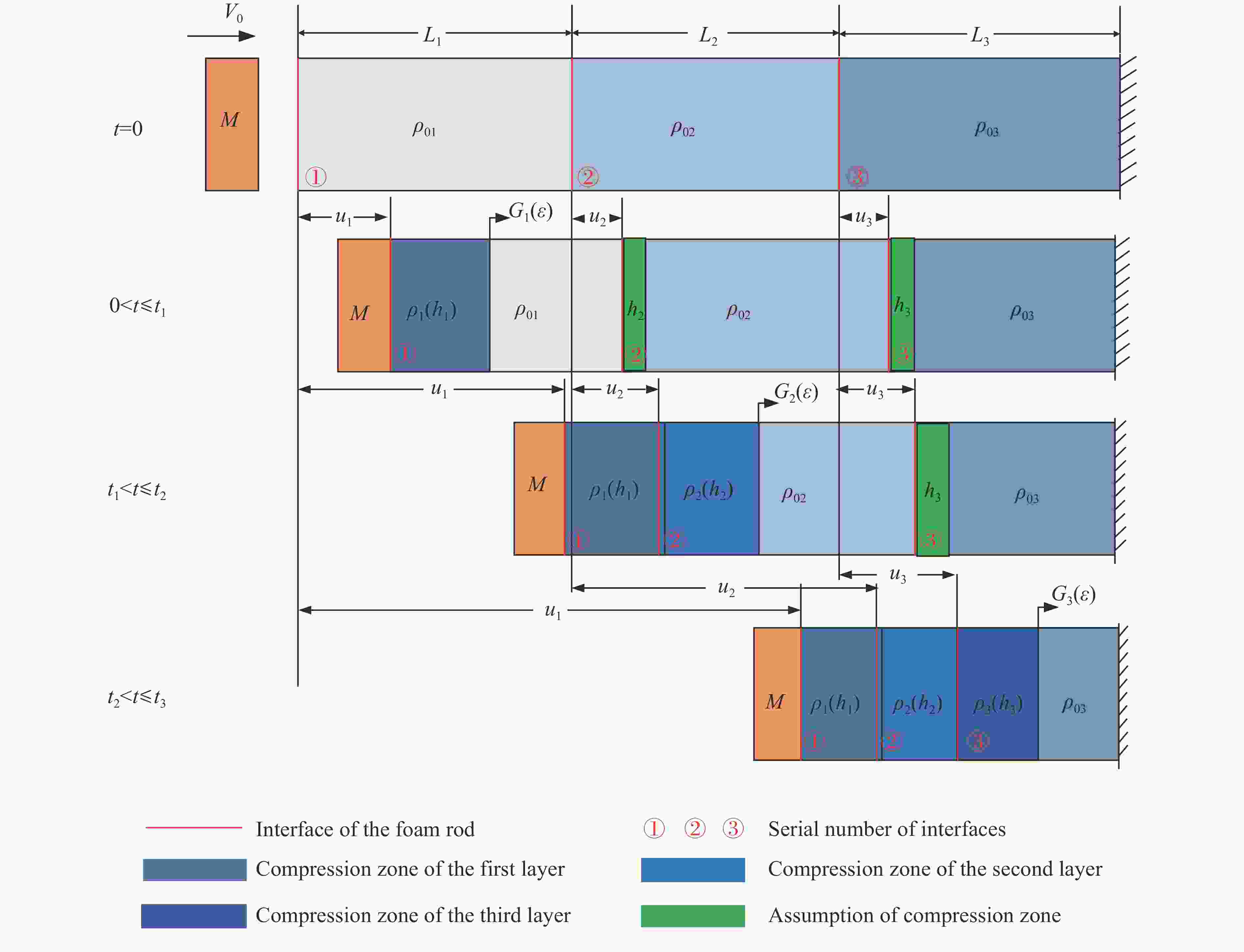
摘要: 以一维应力波传播理论为基础,建立了3层金属泡沫材料受到刚性块撞击时的理论模型,研究了刚性块撞击3层泡沫圆杆时的动力响应过程,从理论上给出了刚性块在撞击过程中的速度衰减规律数值解。利用ANSYS/LS-DYNA分析了受刚性块撞击时塑性应力波在3层泡沫材料中的传播过程,比较了刚性块以及层间界面处节点速度的变化规律。通过对比有限元结果与理论结果发现:理论模型能够较好地预测冲击载荷下分层泡沫材料各界面的速度衰减规律;3层梯度泡沫材料比相同质量的单层均质泡沫材料具有更加高效的吸能和缓冲能力。由于理论假设忽略了反射波以及泡沫材料应变硬化效应的影响,理论解与有限元模拟结果之间存在一定的误差。Abstract: The theoretical mode of velocity attenuation of rigid mass and the stress wave propagation in layered cellular materials under dynamic impact loading has been proposed based on the 1-D wave theory and the dynamic response process of a foam rod strike by a rigid mass has been studied. A finite element (FE) validation has been conducted by employing ANSYS/LS-DYNA software, agreeing well with the theoretical results. The compared results show that the triple layered graded foam material has better impact reduction and energy absorption capacity than the uniform foam with the same mass. Due to the reflected wave and the strain hardening effects not considered in the theoretical model, there are some acceptable errors between the theoretical and FE results.
-
Key words:
- layered cellular material /
- dynamic crushing /
- stress wave /
- theoretical model
-
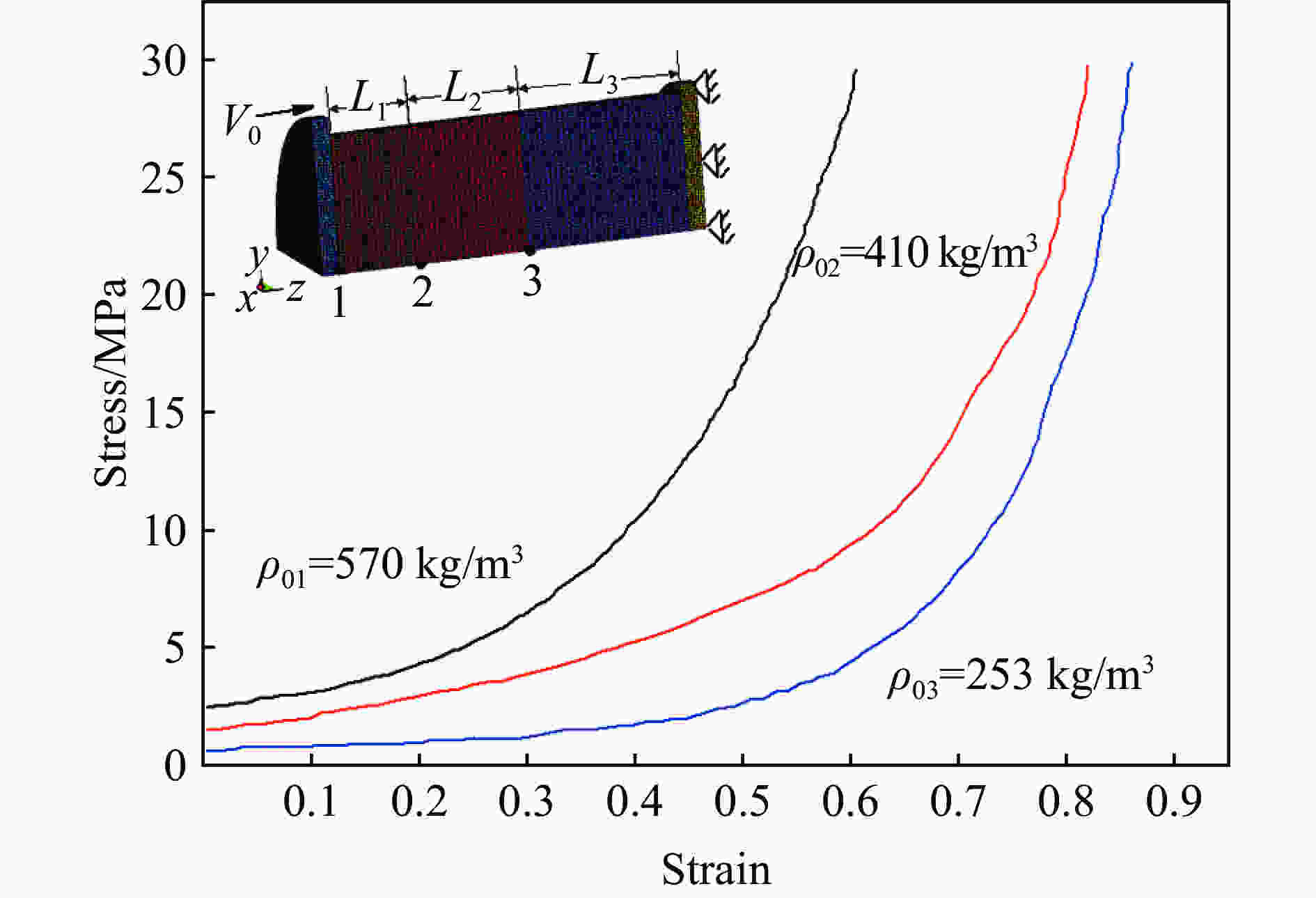
表 1 泡沫杆参数
Table 1. Parameters of the foam rod
L1/mm L2/mm L3/mm ${\rho _{01}}$/(kg·m–3) ${\rho _{02}}$/(kg·m–3) ${\rho _{03}}$/(kg·m–3) 30 40 60 570 410 253 -
[1] MA G W, YE Z Q. Energy absorption of double-layer foam cladding for blast alleviation [J]. International Journal of Impact Engineering, 2007, 34(2): 329–347. doi: 10.1016/j.ijimpeng.2005.07.012 [2] GARDNER N, SHUKLA A. The blast response of sandwich composites with a functionally graded core and polyurea interlayer [M]//Dynamic Behavior of Materials. New York: Springer, 2011: 215–223. [3] WANG E, GARDNER N, SHUKLA A. The blast resistance of sandwich composites with stepwise graded cores [J]. International Journal of Solids and Structures, 2009, 46(18/19): 3492–3502. [4] LI S, LI X, WANG Z, et al. Sandwich panels with layered graded aluminum honeycomb cores under blast loading [J]. Composite Structures, 2017, 173: 242–254. doi: 10.1016/j.compstruct.2017.04.037 [5] LI S, LI X, WANG Z, et al. Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading [J]. Composites Part A: Applied Science and Manufacturing, 2016, 80: 1–12. doi: 10.1016/j.compositesa.2015.09.025 [6] LIU X, TIAN X, LU T J, et al. Blast resistance of sandwich-walled hollow cylinders with graded metallic foam cores [J]. Composite Structures, 2012, 94(8): 2485–2493. doi: 10.1016/j.compstruct.2012.02.029 [7] ZHANG L, HEBERT R, WRIGHT J T, et al. Dynamic response of corrugated sandwich steel plates with graded cores [J]. International Journal of Impact Engineering, 2014, 65: 185–194. doi: 10.1016/j.ijimpeng.2013.11.011 [8] REID S R, PENG C. Dynamic uniaxial crushing of wood [J]. International Journal of Impact Engineering, 1997, 19(5/6): 531–570. [9] TAN P J, REID S R, HARRIGAN J J, et al. Dynamic compressive strength properties of aluminium foams. Part II—‘shock’ theory and comparison with experimental data and numerical models [J]. Journal of the Mechanics and Physics of Solids, 2005, 53(10): 2206–2230. doi: 10.1016/j.jmps.2005.05.003 [10] KARAGIOZOVA D. Velocity attenuation and force transfer by a single-and double-layer claddings made of foam materials [J]. International Journal of Protective Structures, 2011, 2(4): 417–437. doi: 10.1260/2041-4196.2.4.417 [11] GURUPRASAD S, MUKHERJEE A. Layered sacrificial claddings under blast loading Part I—analytical studies [J]. International Journal of Impact Engineering, 2000, 24(9): 957–973. doi: 10.1016/S0734-743X(00)00004-X -






 下载:
下载: