Material Phase Evolution in Hypervelocity Impact Process
-
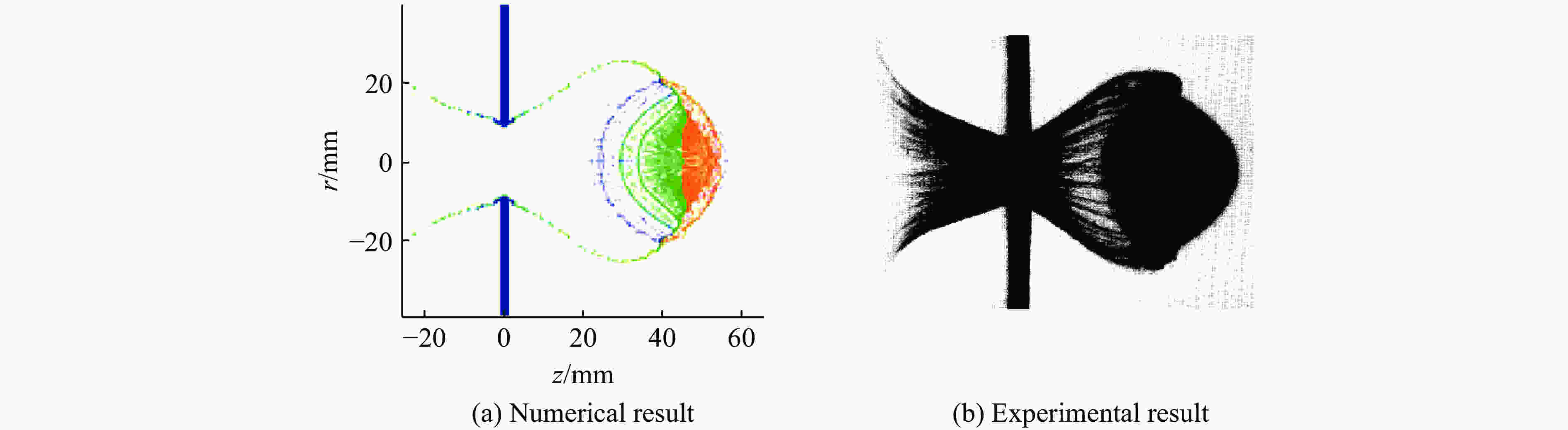
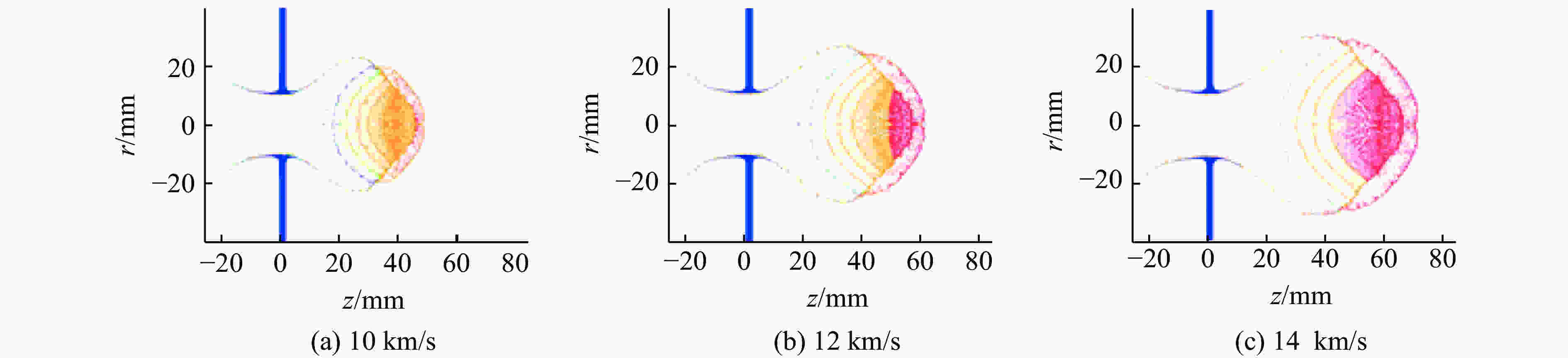
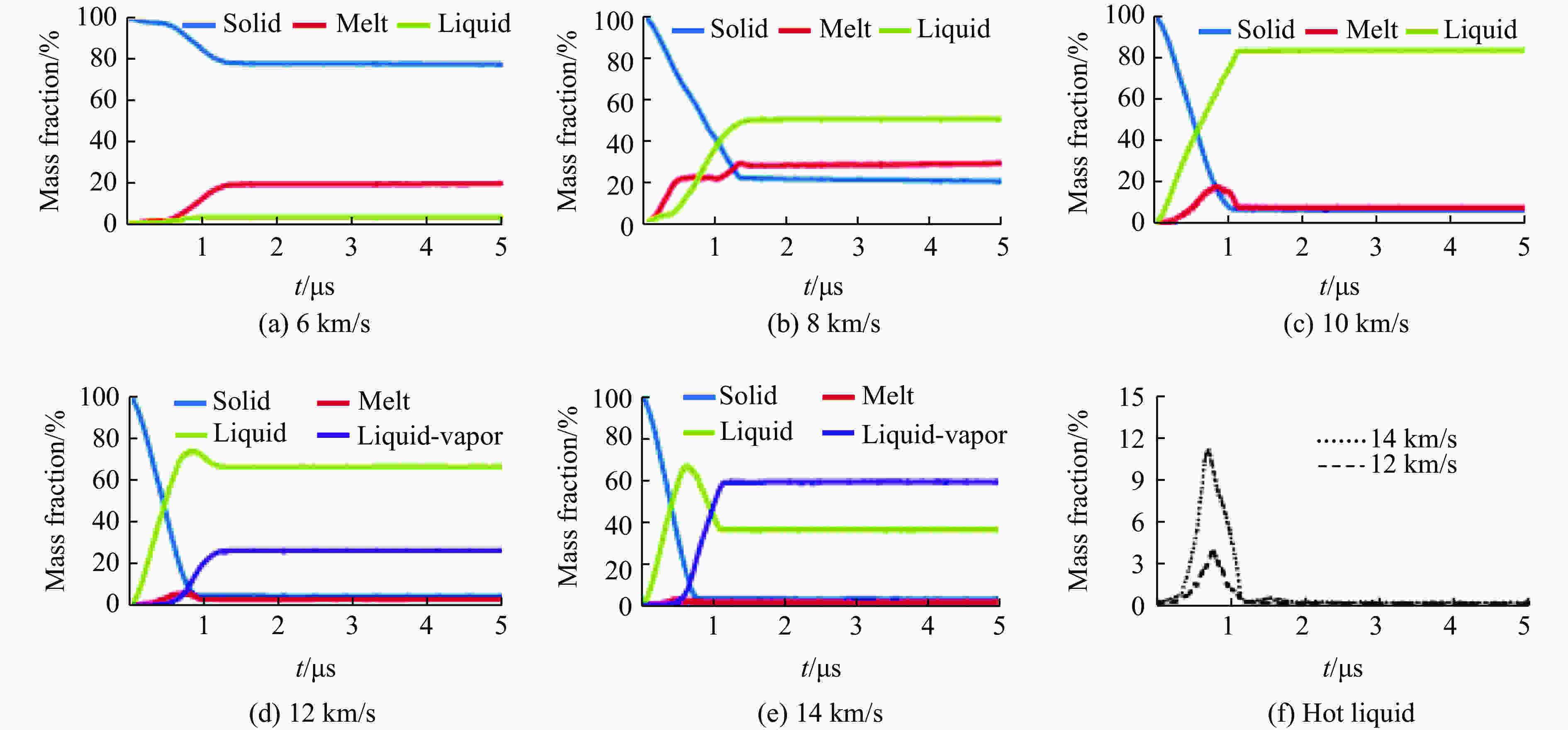
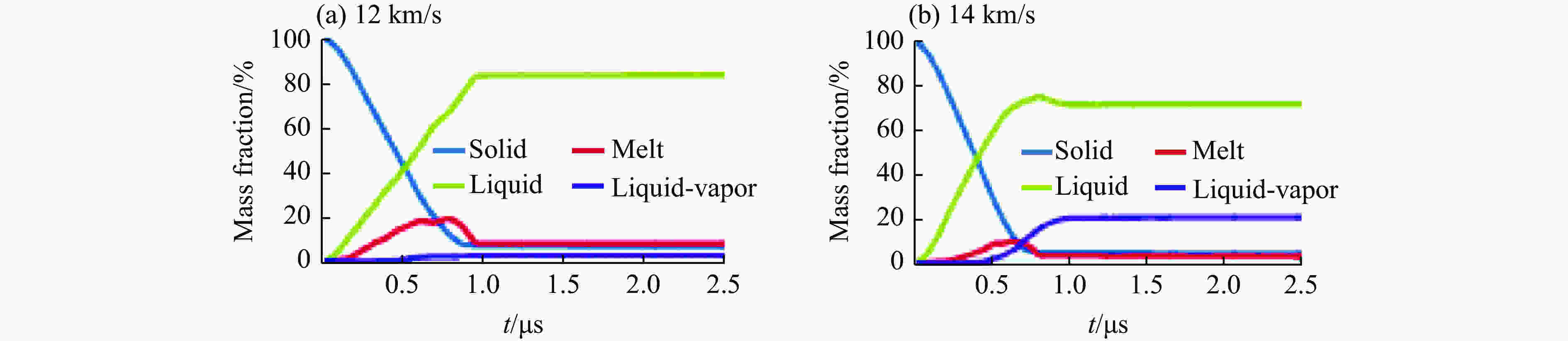
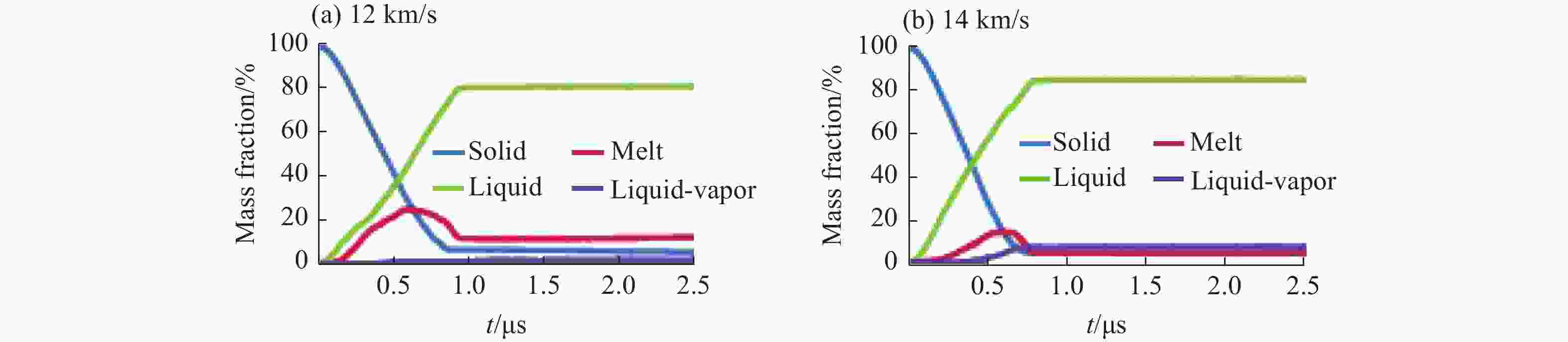
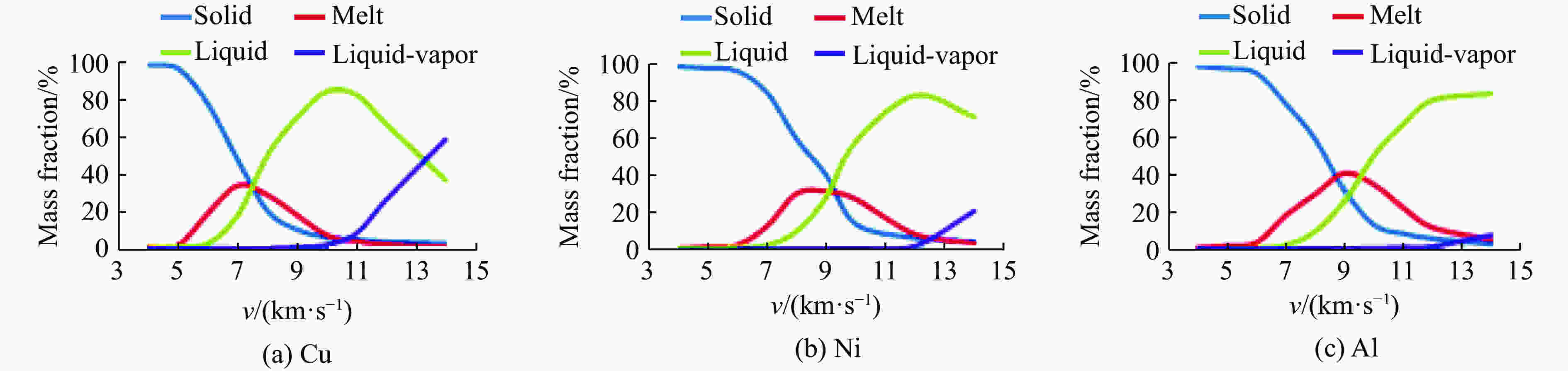
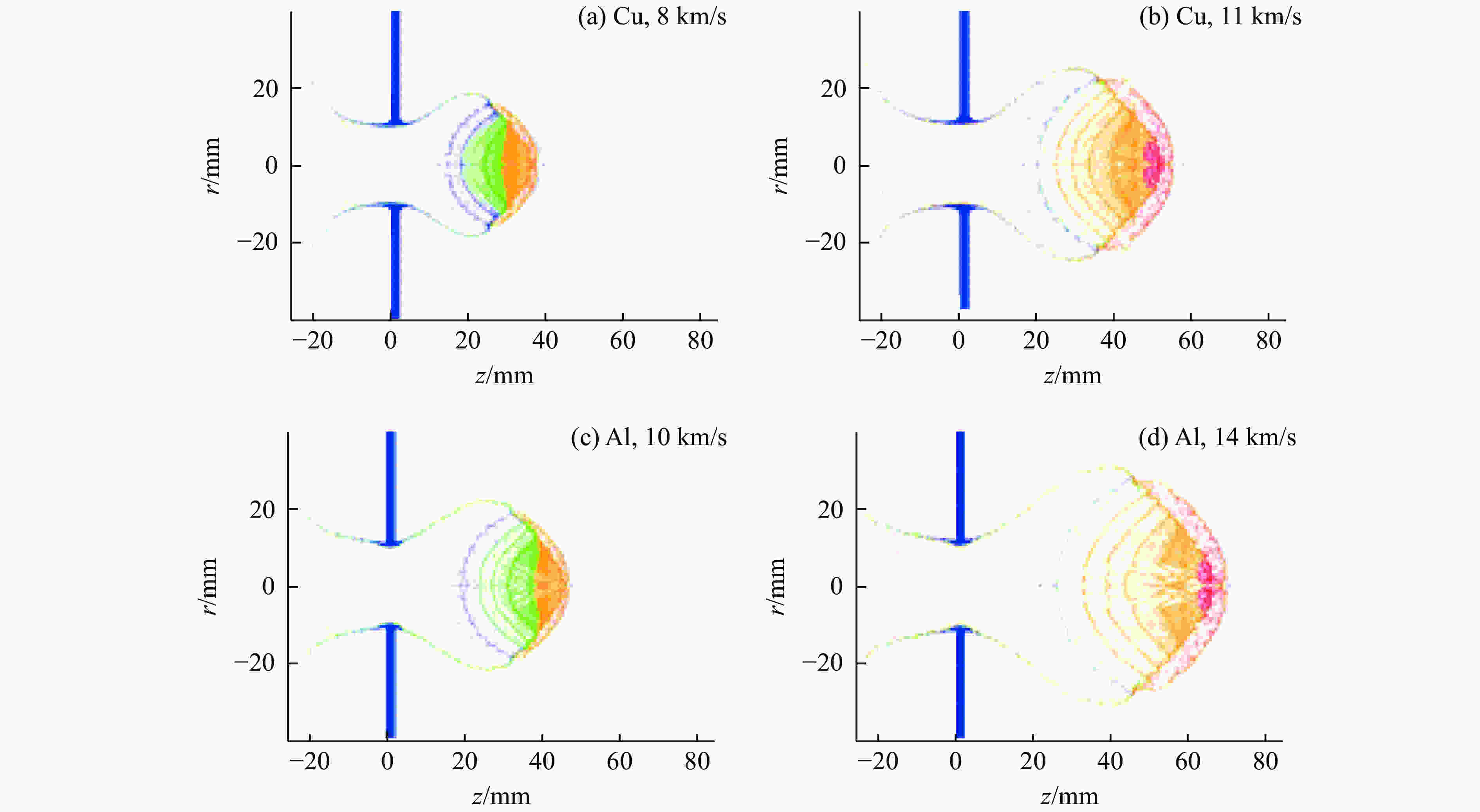
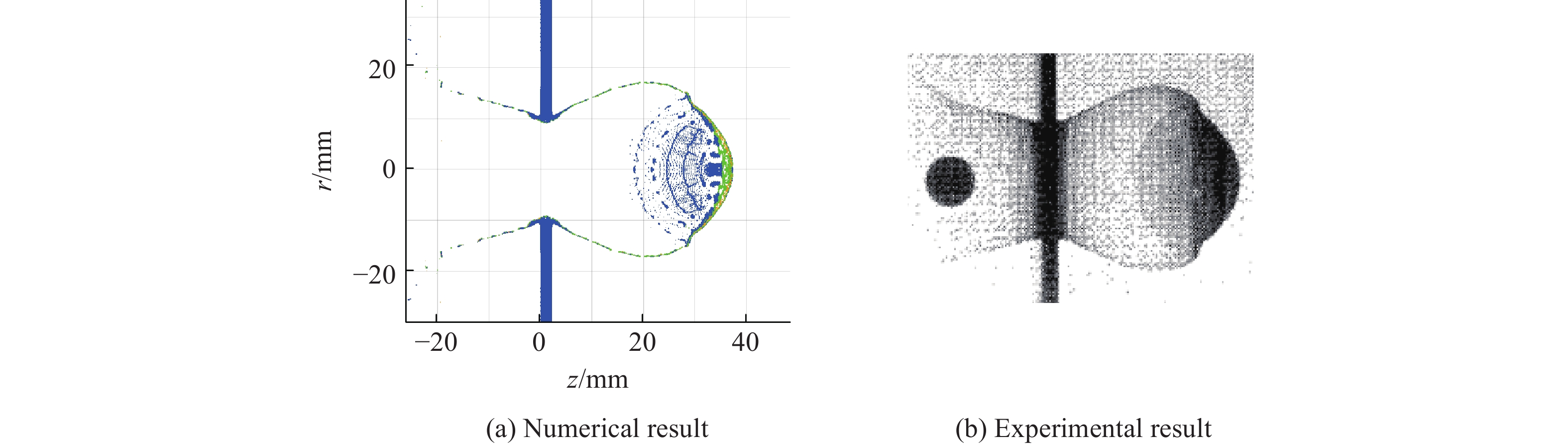
摘要: 在碰撞速度大于10 km/s的超高速碰撞问题中,弹体材料大部分发生液化、汽化,以现有技术手段对此类问题进行实验研究存在一定难度。为深入了解超高速碰撞过程中材料物相的演化规律,揭示不同密度、熔点的材料在超高速碰撞过程中的物相演化特征,采用物质点法,结合GRAY三相物态方程,对铜、镍、铝3种金属材料的超高速碰撞问题进行数值模拟研究,得到不同碰撞速度下弹体材料物相分布随时间变化曲线,并总结出材料特性和碰撞速度对物相演化的影响规律,为开展超高速碰撞等效实验提供参考。Abstract: It is generally known that phase evolution characteristics of materials under hypervelocity impact obtained are limited by experiments. In this paper, the material point method and GRAY three-phase equation of state were combined to simulate the hypervelocity impact of Cu-Cu, Ni-Ni and Al-Al at different velocities, and the relations between phase distribution and time were obtained. The numerical results show that the phase evolution character of the material with higher density and lower melting point at lower velocity impact is similar to the material with lower density and higher melting point at higher velocity impact. Therefore, the phase evolution characteristics of material with higher density and lower melting under hypervelocity impact point could provide reference to the experiment of common structure materials such as Al under hypervelocity impact.
-
Key words:
- hypervelocity impact /
- material point method /
- phase evolution /
- impact velocity
-
表 1 材料参数
Table 1. Material parameters
Material G0/GPa A/MPa B/MPa C n m Al 27.6 265 426 0.015 0.34 1.00 Cu 43.9 90 292 0.025 0.31 1.09 Ni 80.2 163 648 0.006 0.33 1.44 A1 物态方程参数
A1. Parameters of equation of state
Material G/(Pa·cm3·mol–1·K–2) Vb /V0 VJ /V0 ${a_{\rm y}' }$/(GPa·cm6·g–2) M/(g·mol–1) Al 870 0.53 1.347 1 6 450 27.0 Cu 490 0.50 1.401 3 868 63.5 Ni 1 010 0.51 1.407 5 1 190 58.7 -
[1] PIEKUTOWSKI A J. Formation and description of debris clouds produced by hypervelocity impact: NASA Contractor Report 4707 [R]. USA: Marshall Space Flight Center, 1996. [2] POORMON K L, PIEKUTOWSKI A J. Comparisons of cadmium and aluminum debris clouds [J]. International Journal of Impact Engineering, 1995, 17(4/5/6): 639–648. [3] SCHMIDT R M, HOUSEN K R, PIEKUTOWSKI A J, et al. Cadmium simulation of orbital-debris shield performance to scaled velocities of 18 km/s [J]. Journal of Spacecraft and Rockets, 1994, 31(5): 866–877. doi: 10.2514/3.26525 [4] 唐蜜. 基于欧拉方法的超高速撞击程序研制及碎片云物相分布数值模拟[D]. 绵阳: 中国工程物理研究院, 2015: 3–8. [5] MA S, ZHANG X, QIU X M. Comparison study of MPM and SPH in modeling hypervelocity impact problems [J]. International Journal of Impact Engineering, 2009, 36(2): 272–282. doi: 10.1016/j.ijimpeng.2008.07.001 [6] 张雄, 廉艳平, 刘岩, 等.物质点法 [M]. 北京: 清华大学出版社, 2013: 46–50. [7] 汤文辉, 张若棋. 物态方程理论及计算概论 [M]. 2版. 北京: 高等教育出版社, 2008: 159–167. [8] 李依潇, 王生捷. 使用新型物态方程的超高速碰撞物质点法模拟 [J/OL]. 爆炸与冲击 [2019-01-29]. http://kns.cnki.net/kcms/detail/51.1148.O3.20181203.1126.006.html.LI Y X, WANG S J. Simulation of hypervelocity impact by the material point method coupled with a new equation of state [J/OL]. Explosion and Shock Waves [2019–01–29]. http://kns.cnki.net/kcms/detail/51.1148.O3.20181203.1126.006.html. [9] MULLIN S A, ANDERSON JR C E, WILBECK J S. Dissimilar material velocity scaling for hypervelocity impact [J]. International Journal of Impact Engineering, 2003, 29: 469–485. doi: 10.1016/j.ijimpeng.2003.09.043 [10] ROYCE E B. GRAY, a three-phase equation of state for metals: UCRL-51121 [R]. USA: Lawrence Livermore National Laboratory, 1971. -






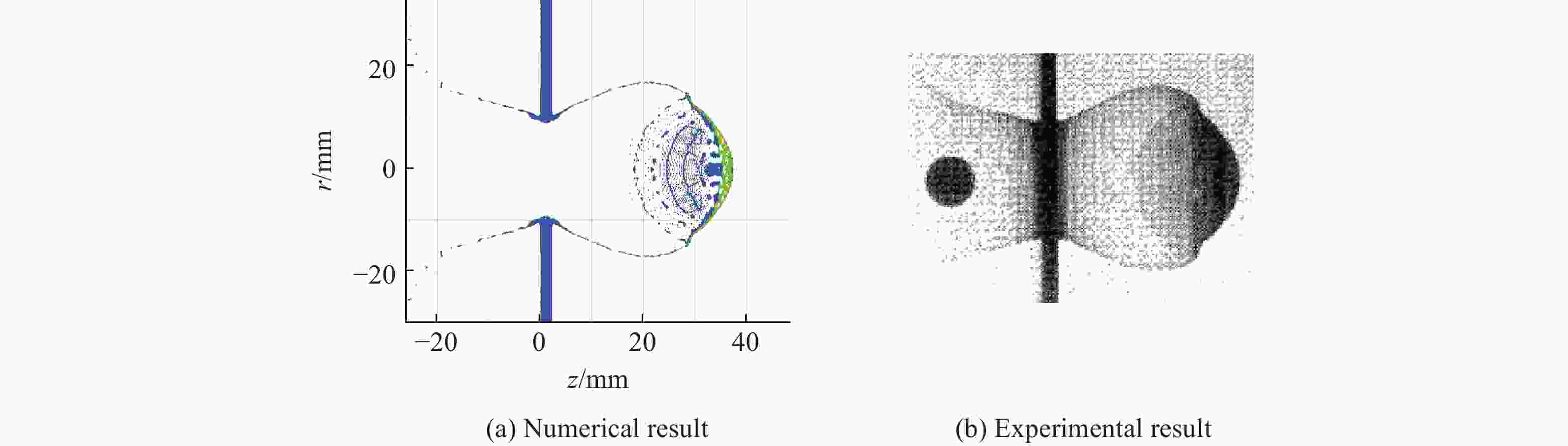
 下载:
下载: