Pressure-Induced Phase Transformations of IrSb from First-Principles Calculations
-
摘要: 基于第一性原理并结合粒子群优化算法的卡里普索（CALYPSO）晶体结构预测方法，研究在0～100 GPa压力下，过渡金属铱和类金属锑组成的化合物IrSb的相变行为和物理性质。研究发现：在常压下，具有立方结构
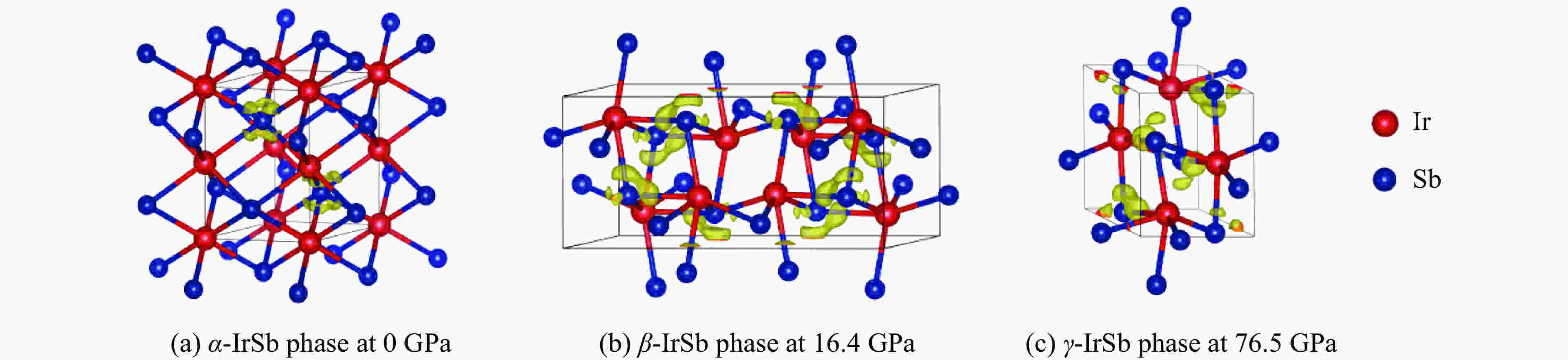
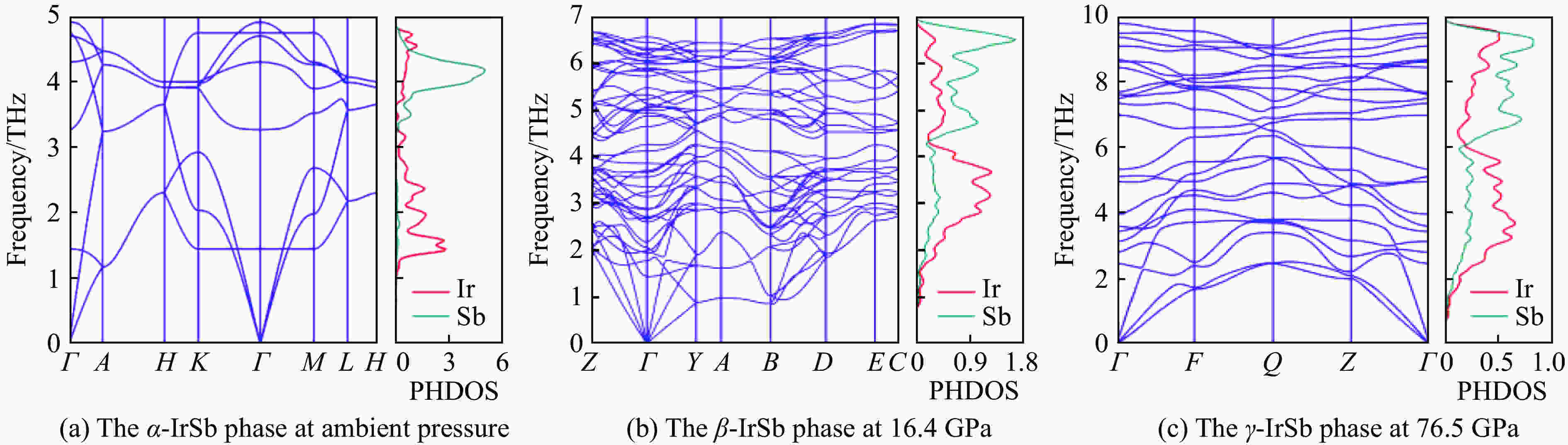
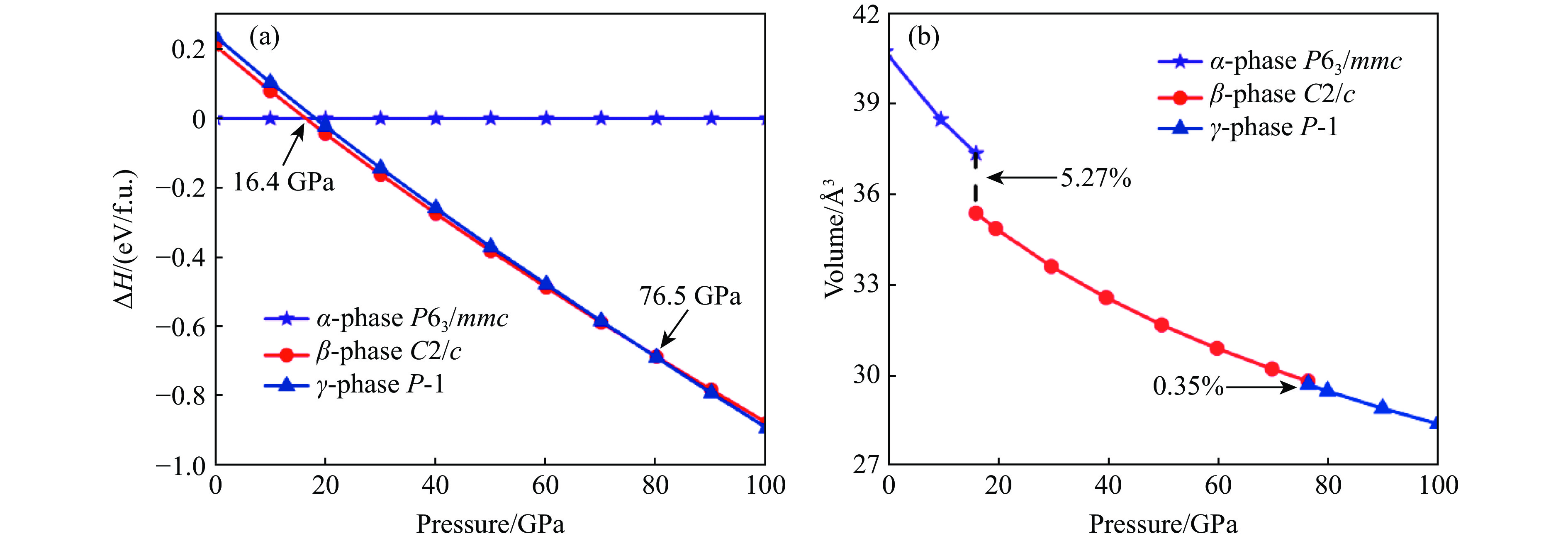
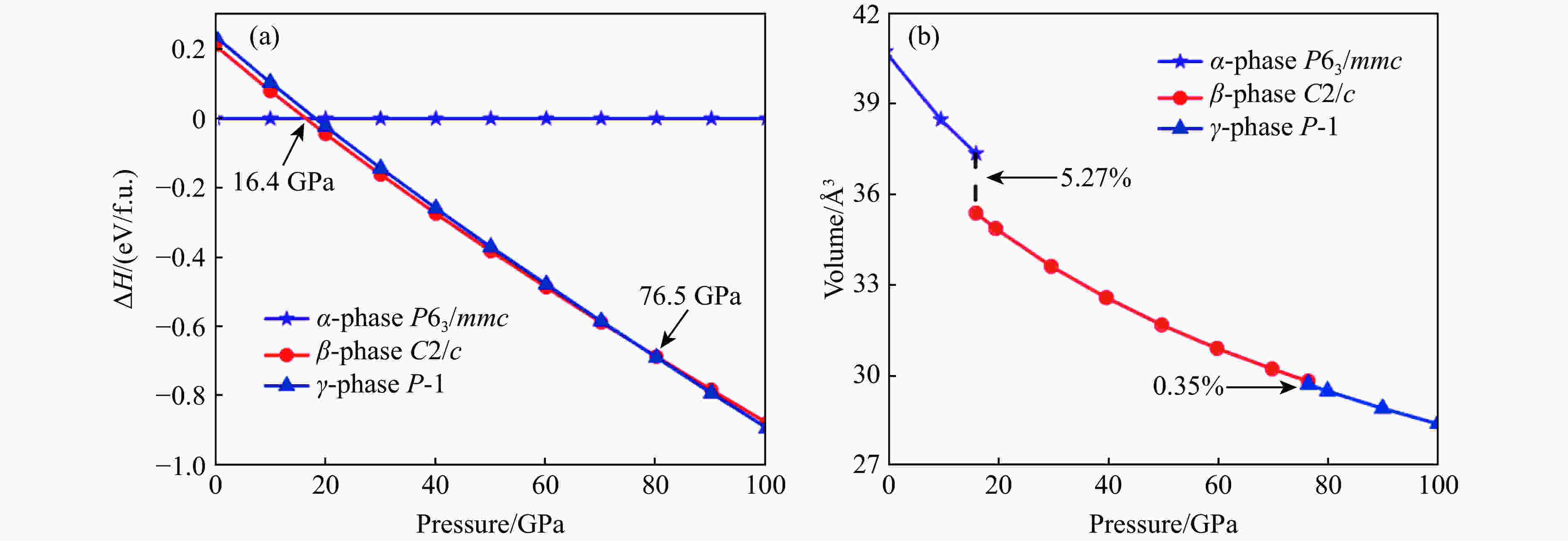
$\alpha $ -IrSb相的空间群为P63/mmc，与实验结果一致；在压力为16.4 GPa时，发现了一种新型立方结构$\beta $ -IrSb相，其空间群为C2/c；在76.5～100 GPa压力范围内，其稳定结构为空间群是P-1的$\gamma $ -IrSb相。声子色散关系计算结果表明：$\alpha $ -IrSb相、$\beta $ -IrSb相和$\gamma $ -IrSb相在各自的布里渊区没有出现虚频，具有动力学稳定性。计算得出3个相的形成焓均小于零，说明3个相均具有热力学稳定性。能带结构计算结果表明：3个相的晶体结构在费米面附近导带和价带均发生交叠，3个相均呈现金属性。计算并讨论了各相的电荷转移情况，研究发现：Ir原子是受主，Sb原子是施主，电荷从Sb原子向Ir原子转移。Abstract: Based on first-principle calculations and the structure prediction method CALYPSO of particle swarm optimization algorithms, phase transition behaviors and physical properties of IrSb in the pressure range of 0–100 GPa have been systematically studied. At ambient pressure, the space group of$\alpha $ -IrSb phase with cubic structure is P63/mmc, in consistency with experimental results. A new cubic structure,$\beta $ -IrSb phase, is found at 16.4 GPa with the space group of C2/c. When the pressure is above 76.5 GPa, the space group becomes P-1. The phonon dispersion shows that$\alpha $ -,$\beta $ - and$\gamma $ -IrSb phases have no virtual frequency in the whole Brillouin zone, thus the three phases are dynamically stable. Calculated results show that the formation enthalpy of three phases are less than zero, indicating that all the three phases have the thermodynamic stability. Band structure calculations show that all the three phases have the overlapping of conduction bands and valence bands near Fermi surface, thus are metallic phases. The charge transfer of each phase is calculated and discussed, in which Ir atoms are the acceptor and Sb atoms are the donor.-
Key words:
- high pressure /
- first-principle calculations /
- crystal structure prediction /
- IrSb
-
图 1 IrSb的热力学焓差曲线（a）以及
$\alpha $ -IrSb相、$\beta $ -IrSb相和$\gamma $ -IrSb相体积随压强变化（b）Figure 1. Calculated enthalpy difference as a function of pressure relative to IrSb （a） and calculated volume versus pressure of
$\alpha $ -IrSb，$\beta $ -IrSb and$\gamma $ -IrSb （b）
图 2
$\alpha $ -IrSb相、$\beta $ -IrSb相和$\gamma $ -IrSb相的晶体结构Figure 2. Crystal structures of
$\alpha $ -IrSb，$\beta $ -IrSb and$\gamma $ -IrSb
图 3
$\alpha $ -IrSb、$\beta $ -IrSb和$\gamma $ -IrSb相的声子色散关系与投影态密度Figure 3. Phonon-dispersion curves and the projected density of states of
$\alpha $ -IrSb，$\beta $ -IrSb, and$\gamma $ -IrSb
图 4
$\alpha $ -IrSb相、$\beta $ -IrSb相和$\gamma $ -IrSb相的能带结构和电子态密度Figure 4. Band structure and partial density of states of
$\alpha $ -IrSb，$\beta $ -IrSb and$\gamma $ -IrSb表 1
$\alpha $ -IrSb相、$\beta $ -IrSb相和$\gamma $ -IrSb的晶格参数和原子位置Table 1. Lattice parameters and atomic coordinates of
$\alpha $ -IrSb,$\beta $ -IrSb and$\gamma $ -IrSbPhase Pressue/GPa Space group Lattice parameters Wyckoff positions $\alpha $-IrSb 0 P63/mmc a=4.082 Å，b=4.082 Å，c=5.634 Å
$\alpha $=90.0°，$\beta $=90.0°，$\gamma $=120.0°Ir1：2a (0, 0, 0) Sb1：2c (0.333, 0.000, 0.500) $\beta $-IrSb 16.4 C2/c a=11.207 Å，b=5.326 Å，c=5.061 Å
$\alpha $=90.0°，$\beta $=110.7°，$\gamma $=90.0°Ir1：8f (0.400, 0.673, 1.361) Sb1：8f (0.000, 0.500, 0.152) $\gamma $-IrSb 76.5 P-1 a=4.812 Å，b=5.034 Å，c=5.033 Å
$\alpha $=98.8°，$\beta $=99.6°，$\gamma $=92.1°Ir1：2i (0.217, 0.525, 0.204) Ir3：2i (0.676, 0.877, 0.183) Sb1：2i (0.200, 0.032, 0.297) Sb3：2i (0.722, 0.393, 0.289) 
下载: 导出CSV
表 2
$\alpha $ -IrSb相、$\beta $ -IrSb相和$\gamma $ -IrSb相的Bader电荷转移Table 2. Calculated Bader charges of
$\alpha $ -IrSb,$\beta $ -IrSb and$\gamma $ -IrSbPhase Pressue/GPa Space group Atom Number Charge value/e $\delta $/e $\alpha $–IrSb 0 P63/mmc Ir 2 9.60 –0.60 Sb 2 4.40 0.60 $\beta $–IrSb 16.4 C2/c Ir 8 9.66 –0.66 Sb 8 4.34 0.66 $\gamma $–IrSb 76.5 P-1 Ir 2 9.64 –0.64 2 9.75 –0.75 Sb 2 4.30 0.70 2 4.31 0.69
下载: 导出CSV
-
[1] HEMLEY R J. Effects of high pressure on molecules [J]. Annual Review of Physical Chemistry, 2000, 51(1): 763–800. doi: 10.1146/annurev.physchem.51.1.763 [2] SCHTTION V, BINI R. Molecules under extreme conditions: chemical reactions at high pressure [J]. Physical Chemistry Chemical Physics, 2003, 5(10): 1951–1965. doi: 10.1039/b301381b [3] GROCCHALA W, HOFFMANN R, FENG J, et al. The chemical imagination at work in very tight places [J]. Cheminform, 2007, 46(20): 3620–3642. [4] CERENIUS Y, DUBROVINSKY L. Compressibility measurements on iridium [J]. Journal of Alloys and Compounds, 2000, 306: 26–29. doi: 10.1016/S0925-8388(00)00767-2 [5] WIBERG E, WIBERGN, HOLLEMAN A F. Inorganic chemistry [M]. Academic Press, 2001. [6] KUZMIN R N. X-ray diffraction study of the structure of IrSb [J]. Soviet Physics, Crystallography, 1958, 3(3): 366–368. [7] ZHURAVLEV N N, ZHDANOV G S. X-ray diffraction determination of the structure of CoSb3, RhSb3, and IrSb3 [J]. Soviet Physics, Crystallography, 1956, 1(5): 404. [8] HULLIGER F. Semiconducting compounds with skutterudite structure [J]. Helvetica Physica Acta, 1961, 34: 782–786. [9] GLEN A, SLACK, VENETA G, TSOUKALA. Some properties of semiconducting IrSb3 [J]. Journal of Applied Physics, 1994, 76: 1665. doi: 10.1063/1.357750 [10] 杨明宇, 杨倩, 张勃, 等. 5d过渡金属原子掺杂六方氮化铝单层的磁性及自旋轨道耦合效应:可能存在的二维长程磁有序 [J]. 物理学报, 2017, 66(6): 063102.YANG M Y, YANG Q, ZHANG B, et al. Electronic structures, magnetic properties and spin-orbital coupling effects of aluminum nitride monolayers doped by 5d transition metal atoms: possible two-dimensional long-range magnetic orders [J]. Acta Physica Sinica, 2017, 66(6): 063102. [11] WANG Y, LV J, ZHU L, et al. Crystal structure prediction via particle swarm optimization [J]. Physics, 2010, 82(9): 7174–7182. [12] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758–1775. doi: 10.1103/PhysRevB.59.1758 [13] KRESSE G, HAFNERR J. Ab initio molecular-dynamics simulation of the liquid-metal; amorphous-semiconductor transition in germanium [J]. Physical Review B, 1994, 49(20): 14251–14269. doi: 10.1103/PhysRevB.49.14251 [14] KRESSE G, HAFNERR J. Ab initio molecular dynamics for liquid metals [J]. Physical Review B, 1993, 47(1): 558–561. doi: 10.1103/PhysRevB.47.558 [15] PHILLIPS J C. Energy-band interpolation scheme based on a pseudopotential [J]. Physical Review, 1958, 112(3): 685–695. doi: 10.1103/PhysRev.112.685 [16] 陈舜麒.计算材料科学 [M]. 北京: 化学工业出版社, 2005: 100–105.CHEN S L. Computational materials science [M]. Beijing: Chemical Industry Press, 2005: 100–105. [17] JOHN P P, KIERON B, MATTHIAS E. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865 [18] MONKHORST H J, PACNK J D. Special points for Brillouin-zone integrations [J]. Physical Review B, 1976, 16(4): 1746–1747. [19] THIRUMALAI D, HALL R W, BERNE B. A path integral Monte Carlo study of Liquid neon and the quantum effective pair potential [J]. The Journal of Chemical Physics, 1984, 81(6): 2523–2527. doi: 10.1063/1.447985 [20] BORN M, HUANG K, LAX M. Dynamical theory of crystal lattices [J]. American Journal of Physics, 1956, 23(7): 474–483. [21] WANG Y C, LV J, MA Y M, et al. Superconductivity of MgB2 under ultrahigh pressure: a first-principles study [J]. Physical Review B, 2009, 80(9): 092505. doi: 10.1103/PhysRevB.80.092505 [22] XU L F, ZHAO Z S, WANG L M, et al. Prediction of a three-dimensional conductive superhard material: diamond-like BC2 [J]. The Journal of Physical Chemistry C, 2010, 114(51): 22688–22690. doi: 10.1021/jp106926g [23] BADER R F. Atoms in molecules [J]. Accounts of Chemical Research, 1985, 18(1): 9–15. doi: 10.1021/ar00109a003 [24] OGANOV A R, CHEN J, GATTI C, et al. Ionic high-pressure form of elemental boron [J]. Nature, 2009, 460(7252): 863–868. -
下载:
点击查看大图
计量
- 文章访问数: 8079
- HTML全文浏览量: 3221
- PDF下载量: 46
