Dynamic Behavior of PZT-5 Piezoelectric Ceramics under Impact Loading
-
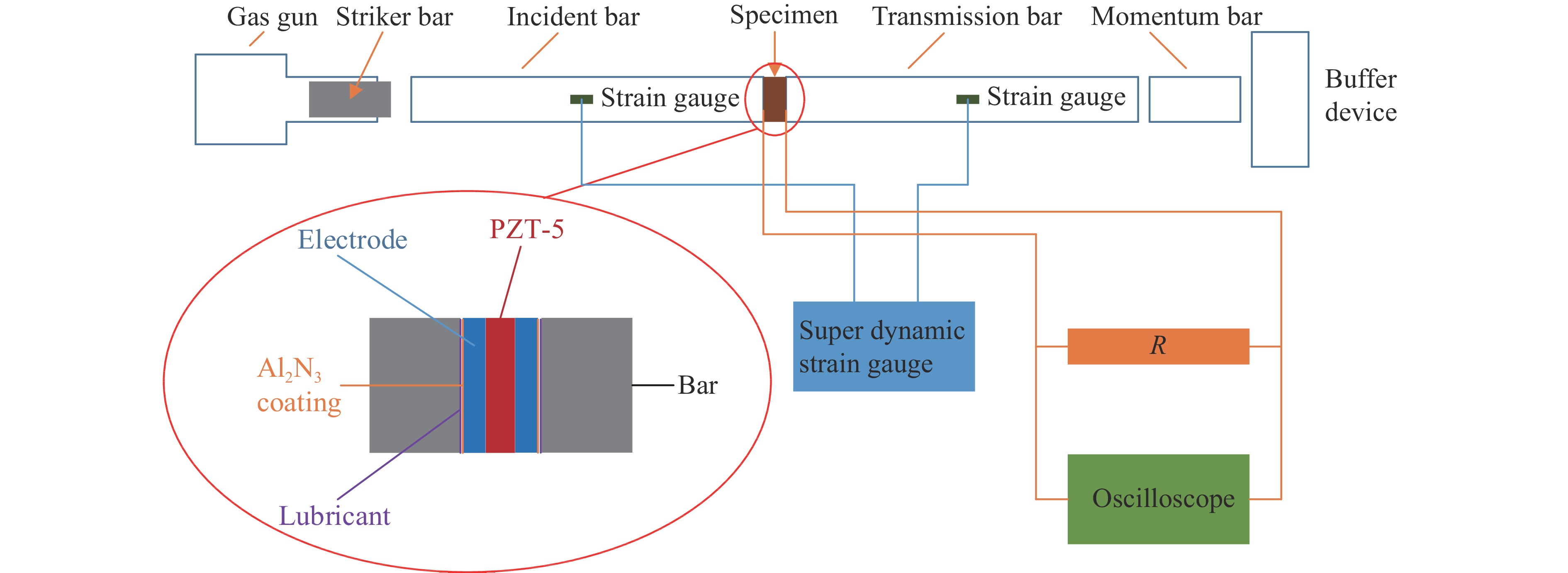
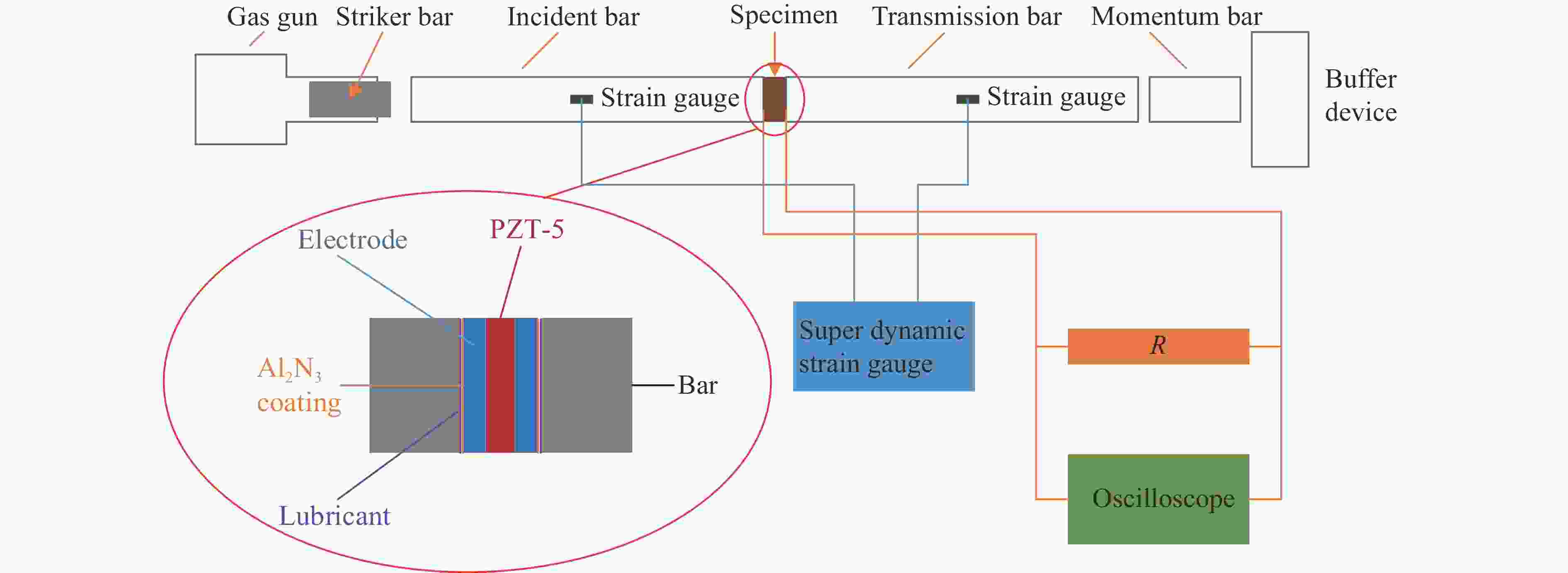
摘要: 压电陶瓷是压电冲击传感器的核心元件。采用分离式霍普金森压杆(SHPB)实验技术研究PZT-5压电陶瓷在冲击载荷作用下的力电特性,进行了4~14 m/s不同速度的实验。实验中为保证试件与压杆绝缘,采用了对试件影响较小的表面溅射Al2N3的工艺,溅射厚度为1~3
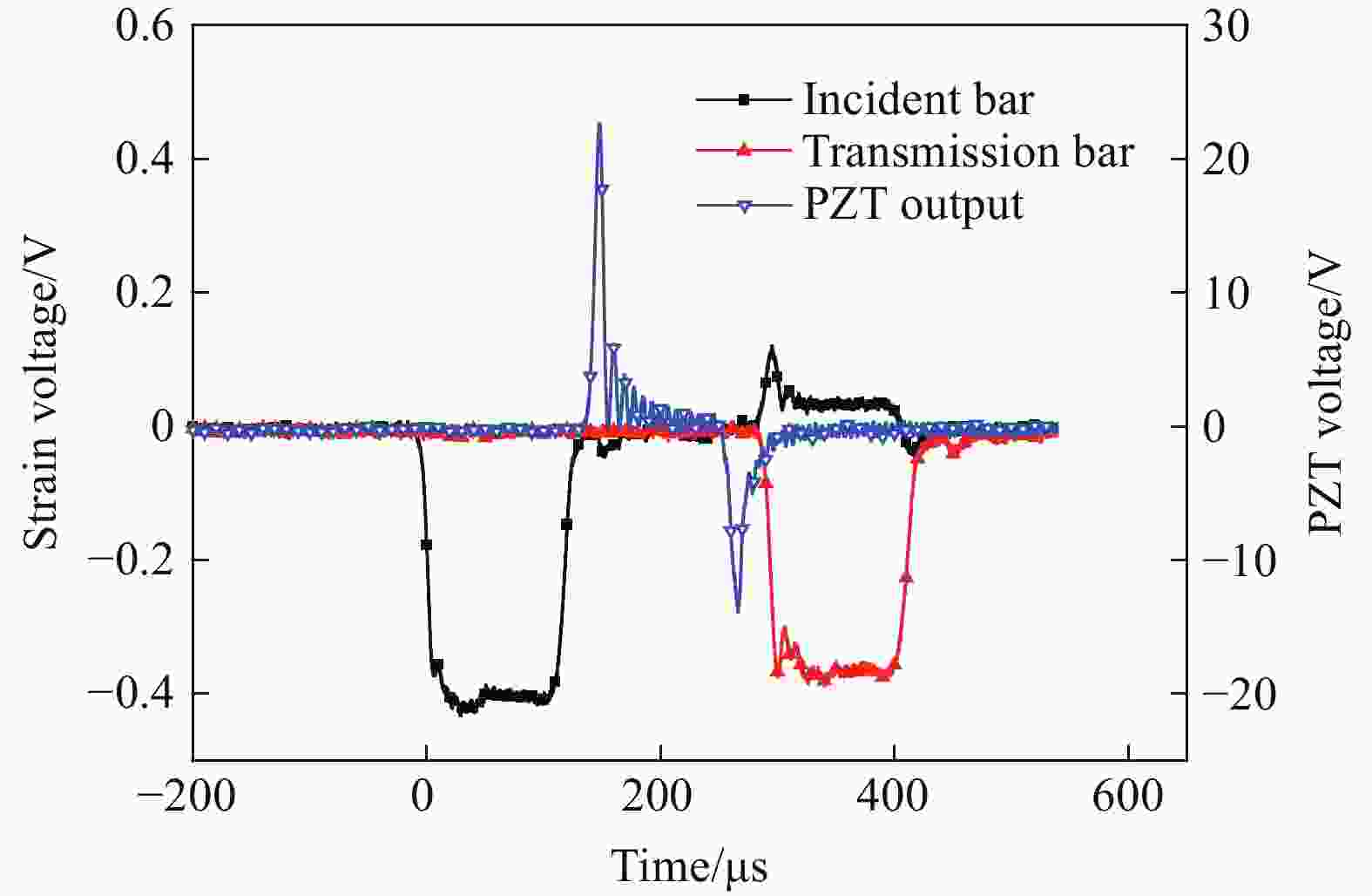
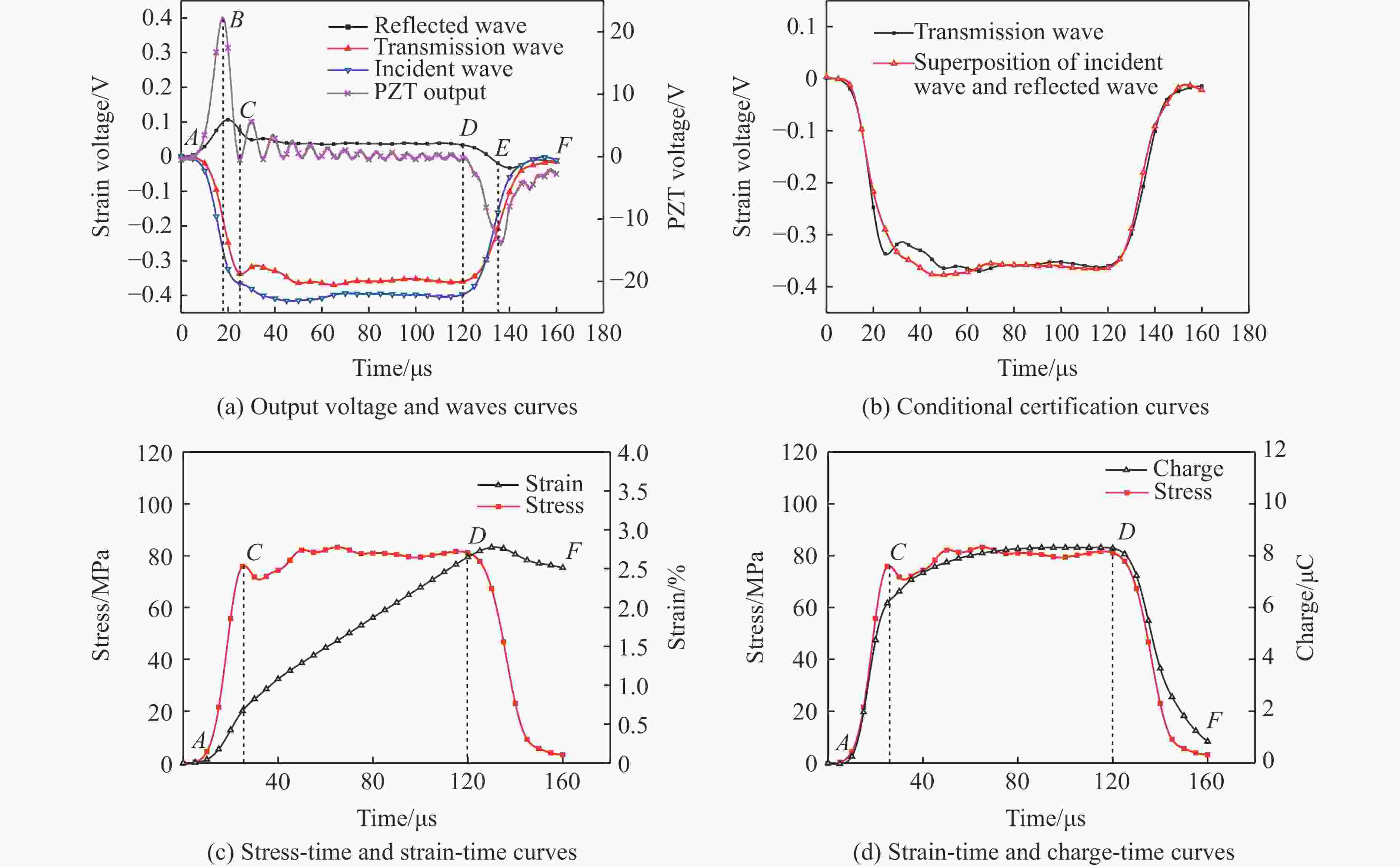
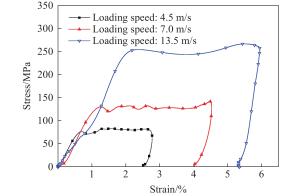
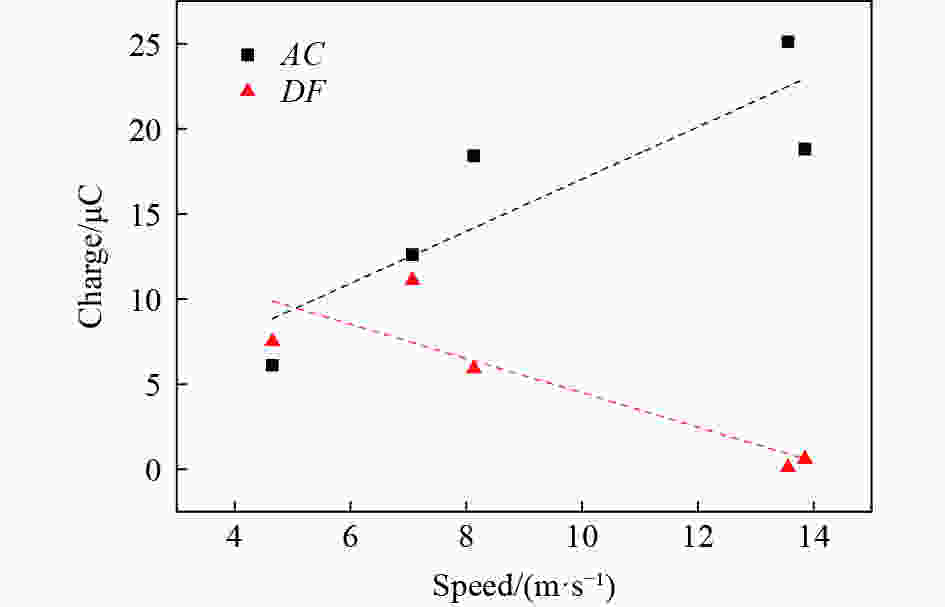
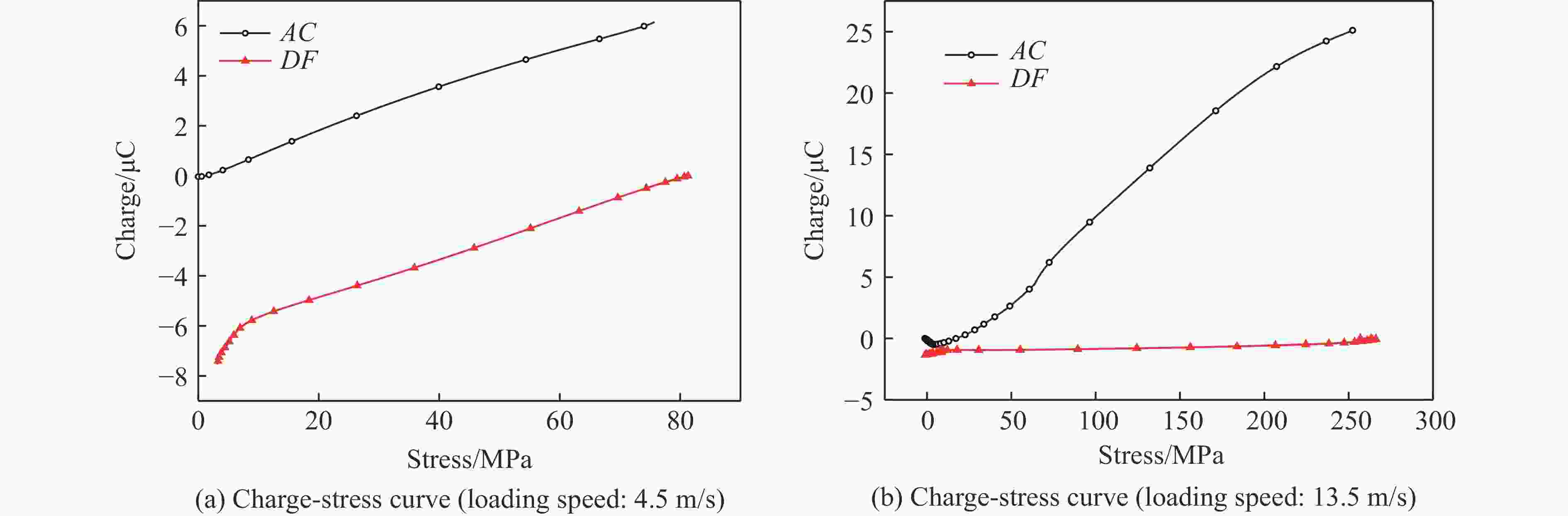
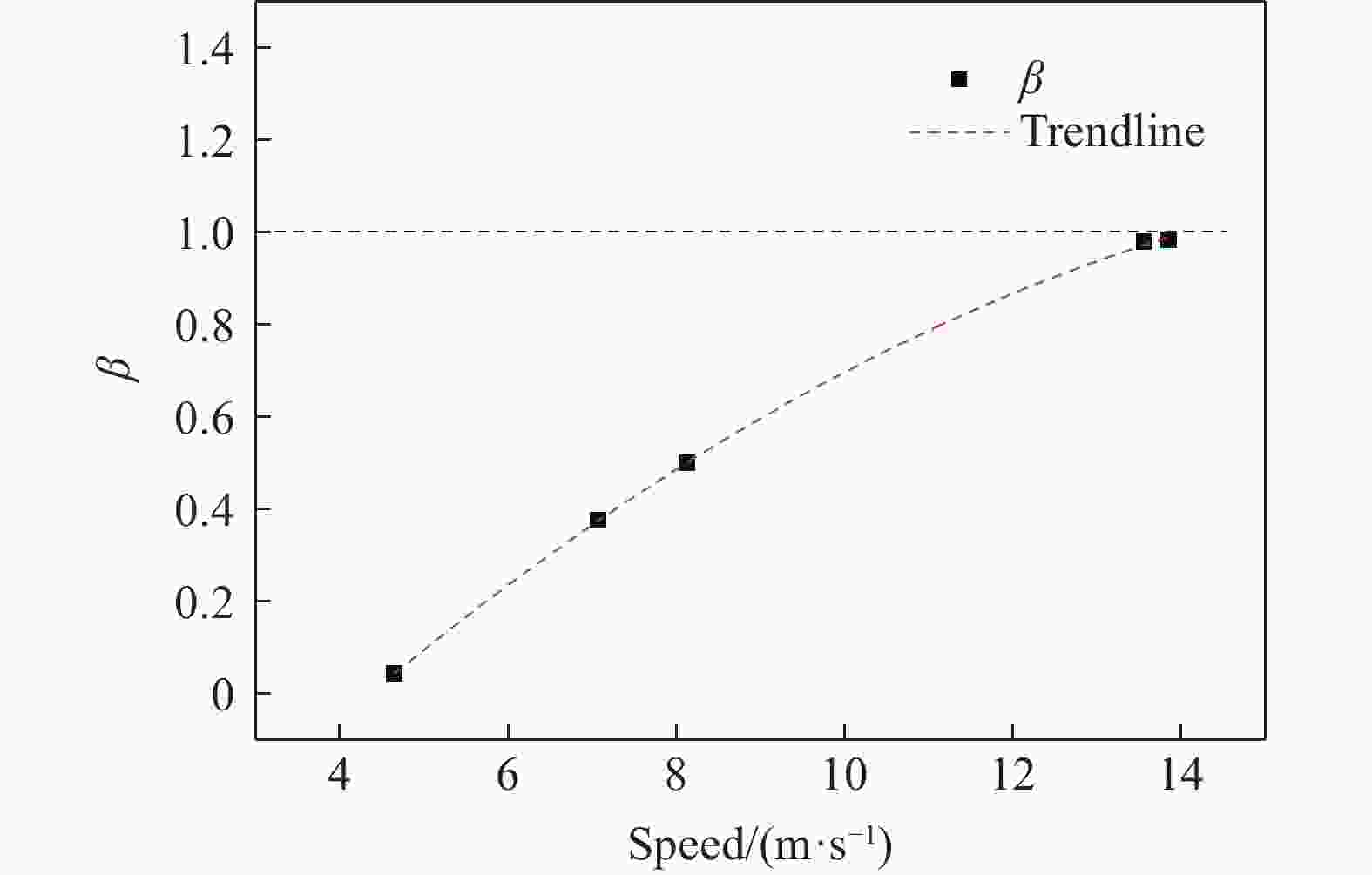
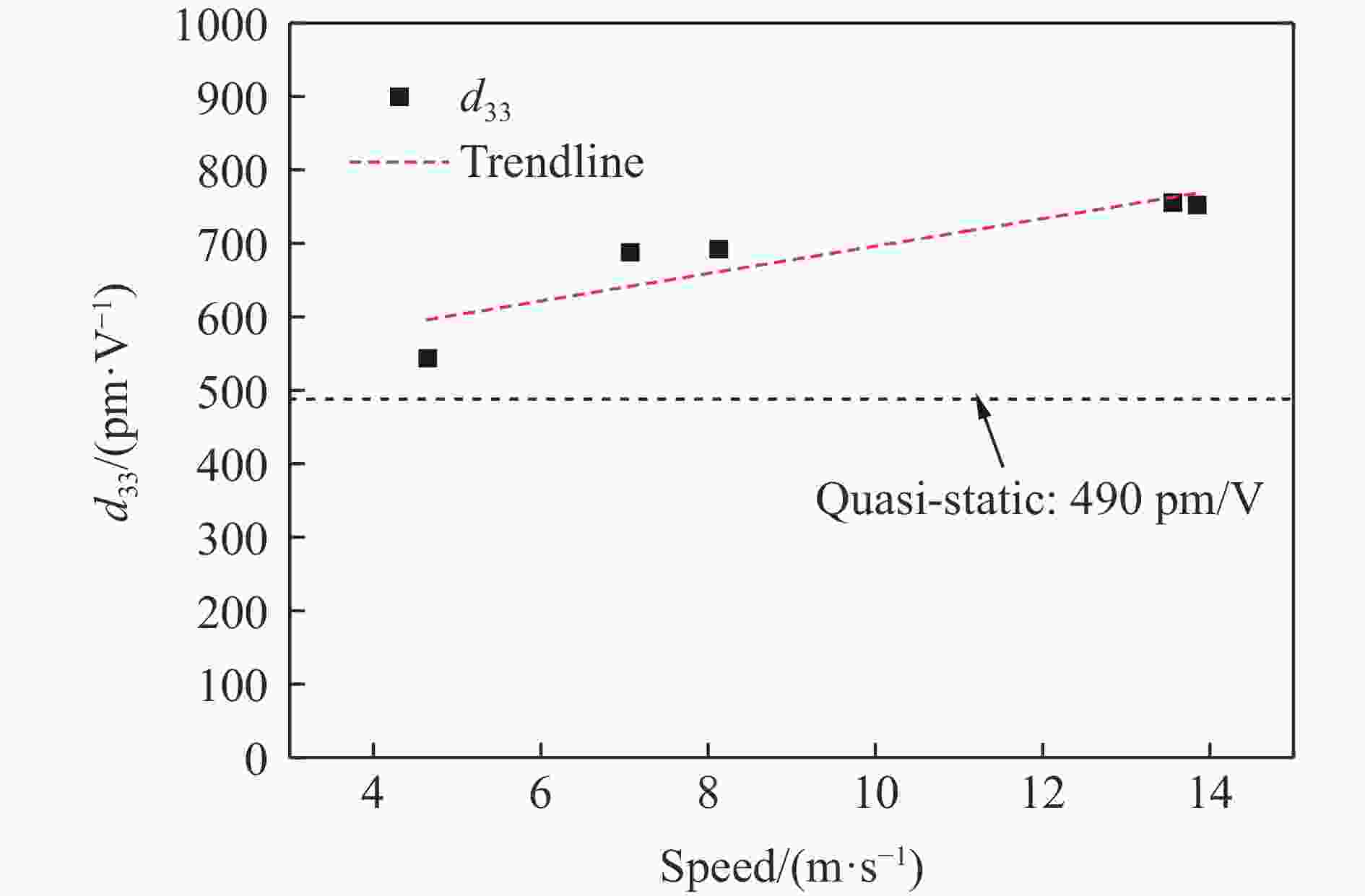
${{\text{μ}}{\rm{m}}}$ 。实验结果表明:在冲击加载过程中,PZT-5压电陶瓷的应变变化表现出黏性性质,其产生的电荷与加载过程中试件的应力、应变均相关;当加载速度超过一定值时,加载过程中压电陶瓷可能产生损伤,不同的损伤程度也影响电荷的产生;PZT-5压电陶瓷的力学和电学性能具有明显的率相关性。Abstract: Piezoelectric ceramics are the core components of piezoelectric impact sensors. The mechanical and electrical behaviors of PZT-5 piezoelectric ceramics were studied by split Hopkinson pressure bar (SHPB) experimental technique. The tests were carried out at speeds of 4–14 m/s. In order to ensure the insulation between specimen and pressure bar, a process of sputtering Al2N3 on the surface that with less influence on the test piece was used, and the sputtering thickness was 1–3${{\text{μ}}{\rm{m}}}$ . The experimental results of SHPB were analyzed and discussed. The results show that the strain change of PZT-5 piezoelectric ceramics exhibits viscous properties during impact loading, and the charge generated is related to the stress and strain of the specimen during loading. When the loading speed exceeds a certain level, the piezoelectric ceramic may be damaged during the loading process, and the degree of damage also affects the generation of charge. The mechanical and electrical properties of PZT-5 piezoelectric ceramics have obvious rate correlation. -
-
[1] 张福学, 王丽坤. 现代压电学(下册) [M]. 北京: 科学出版社, 2001: 337.ZHANG F X, WANG L K. Modern piezoelectricity (Volume 3) [M]. Beijing: Science Press, 2001: 337. [2] 张智丹, 纪松, 张延松. 冲击载荷下PVDF和PZT压电材料的动态性能研究 [J]. 兵器材料科学与工程, 2008, 31(2): 65–69. doi: 10.3969/j.issn.1004-244X.2008.02.018ZHANG Z D, JI S, ZHANG Y S. Research of dynamic behavior of PVDF and PZT piezoelectric materials under shock loading [J]. Ordnance Material Science and Engineering, 2008, 31(2): 65–69. doi: 10.3969/j.issn.1004-244X.2008.02.018 [3] HU J, TJIU N. Dependence of electric energy output from a lead zirconate titanate ceramic piezoelectric element on impact conditions [J]. Materials Chemistry and Physics, 2011, 128(1/2): 172–176. [4] CHURE M C, WU L, WU K K, et al. Power generation characteristics of PZT piezoelectric ceramics using drop weight impact techniques effect of dimensional size [J]. Ceramics International, 2014, 40(1): 341–345. doi: 10.1016/j.ceramint.2013.06.007 [5] 龚双. 层合压电结构的瞬态响应和波动特性分析[D]. 长沙: 湖南大学, 2013.GONG S. Transient response and characteristic waves of layered piezoelectric structures [D]. Changsha: Hunan University, 2013. [6] SHEN Y N, ZHENG Y B. Full transient modelling for piezoelectric actuator with contact-impact [C]//Symposium on Piezoelectricity, Acoustic Waves, and Device Applications, 2014: 98–101. [7] 钱霖, 张峰, 徐先洋, 等. 冲击荷载下PZT5电畴翻转研究 [J]. 功能材料与器件学报, 2017, 48(7): 93–97.QIAN L, ZHANG F, XU X Y, et al. Researches of PZT5 in domain switching under impact loading [J]. Journal of Functional Materials and Devices, 2017, 48(7): 93–97. [8] 董新龙, 周广宇, 祁振林, 等. 冲击压缩下PZT铁电陶瓷本构特性的实验研究[C]//中国力学学会学术大会, 2005: 168.DONG X L, ZHOU G Y, QI Z L, et al. Experimental study on constitutive properties of PZT ferroelectric ceramics under impact compression [C]// Academic Conference on Mechanics of China, 2005: 168. [9] KHAN A S, PROUD W G. Temperature and strain rate effects on the piezoelectric charge production of PZT 95/5 [C]//AIP Conference Proceedings 1793, 2017: 1–5. [10] 王礼立. 应力波基础 [M]. 第2版. 北京: 国防工业出版社, 2005: 53.WANG L L. Foundation of stress waves [M].2nd ed. Beijing: National Denfense Industry Press, 2005: 53. -








 下载:
下载: