Deformation and Energy Absorption of Multi-Hierarchical Sandwich Structures
-
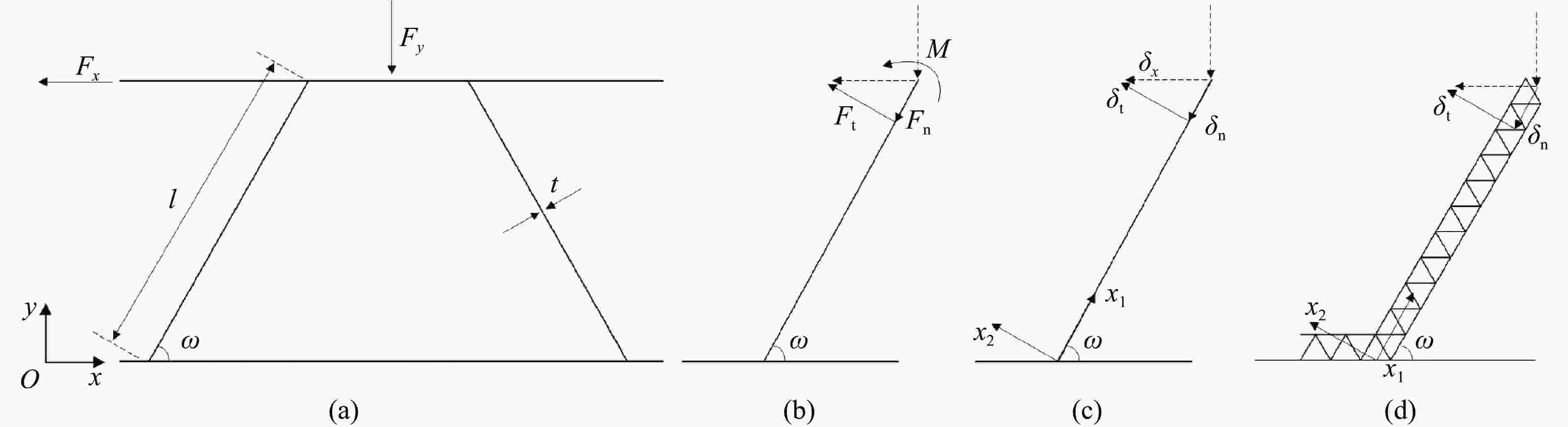
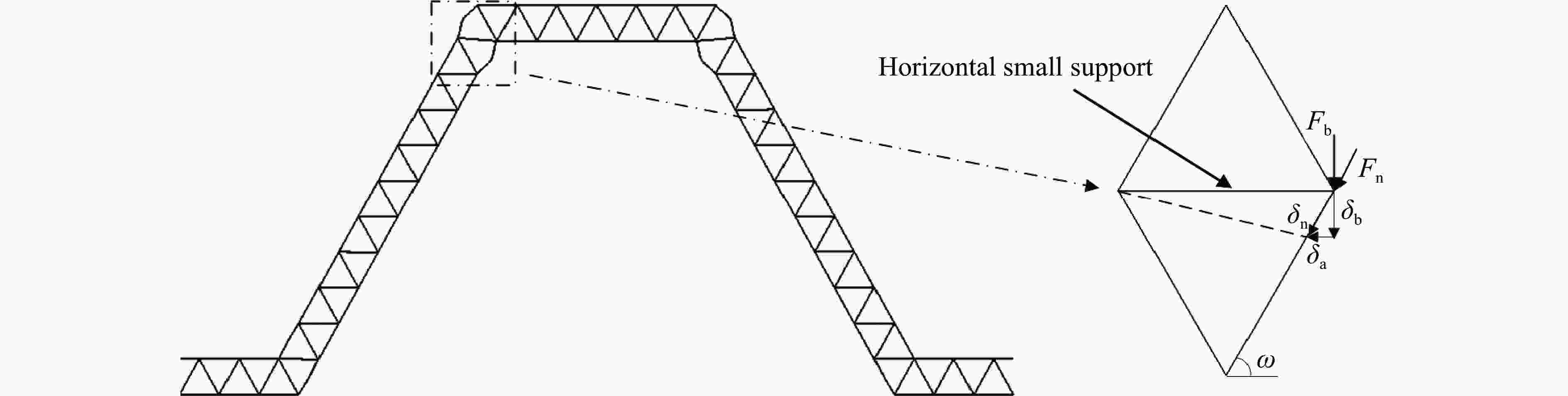
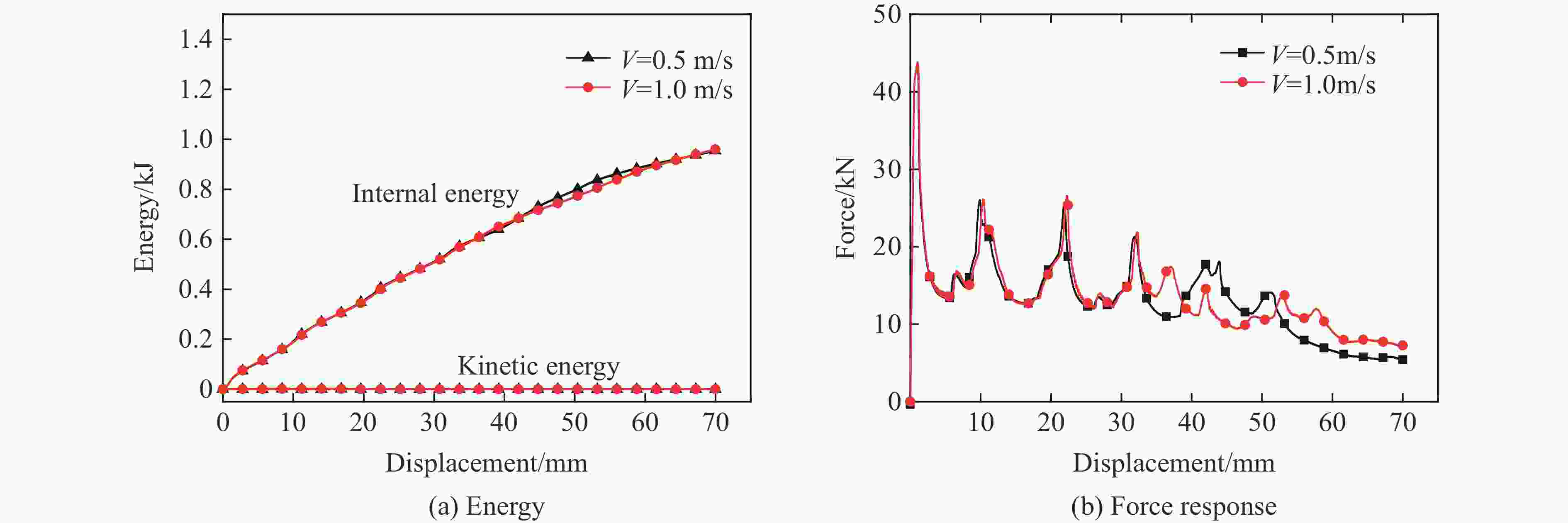
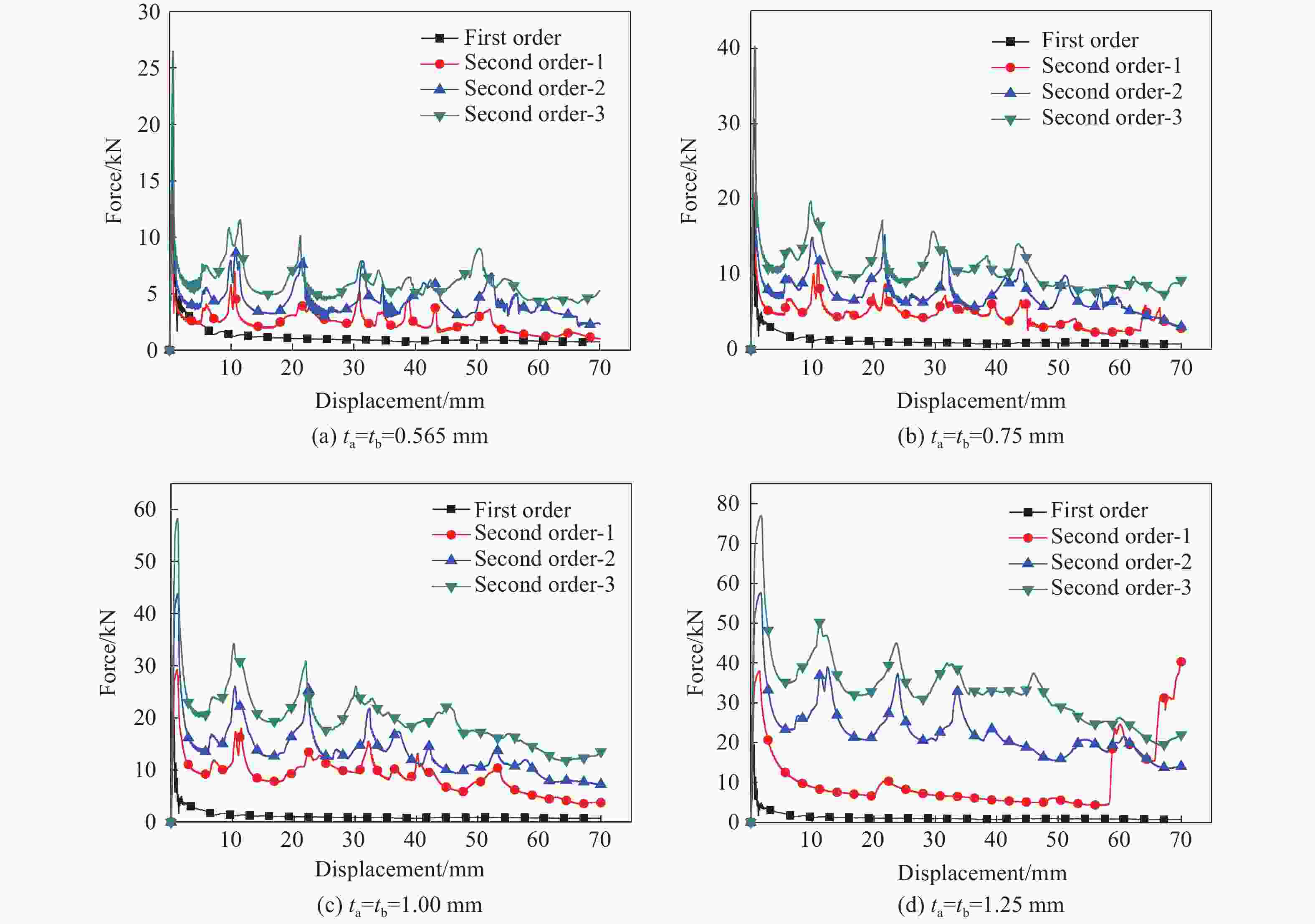
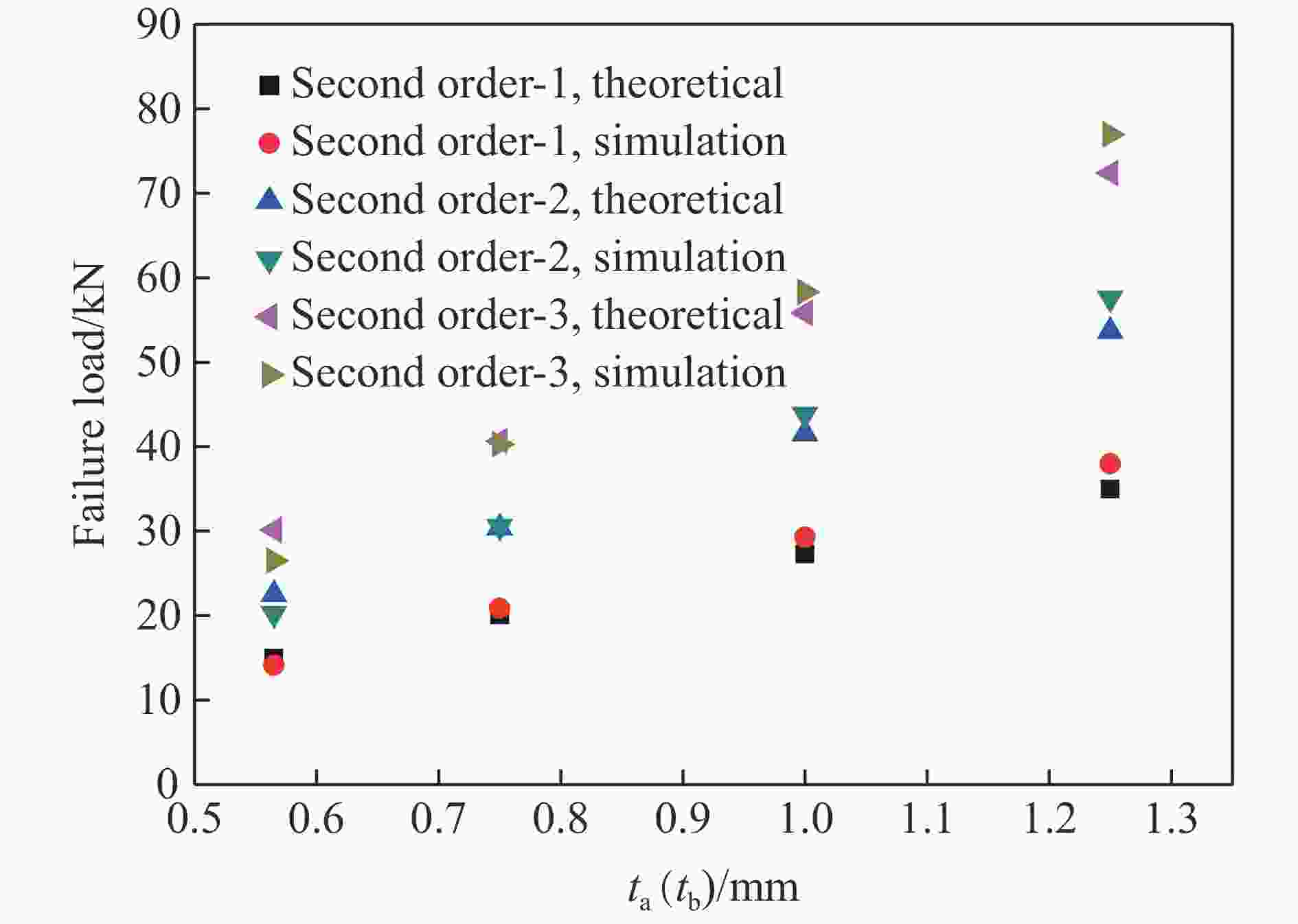
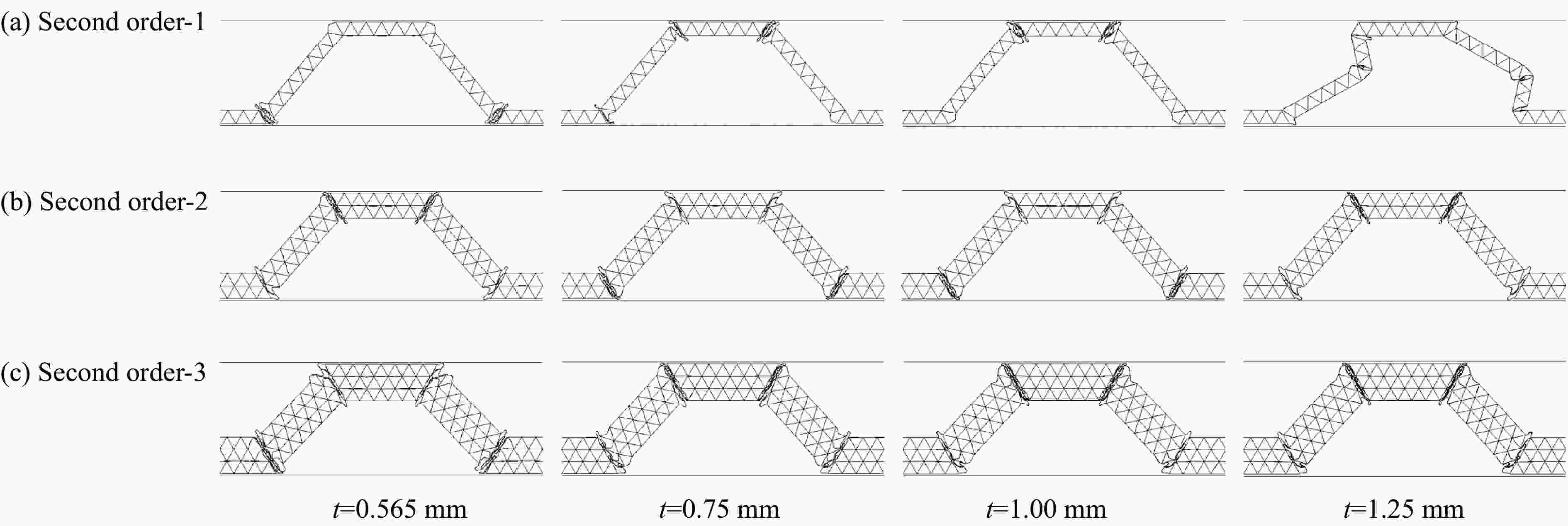
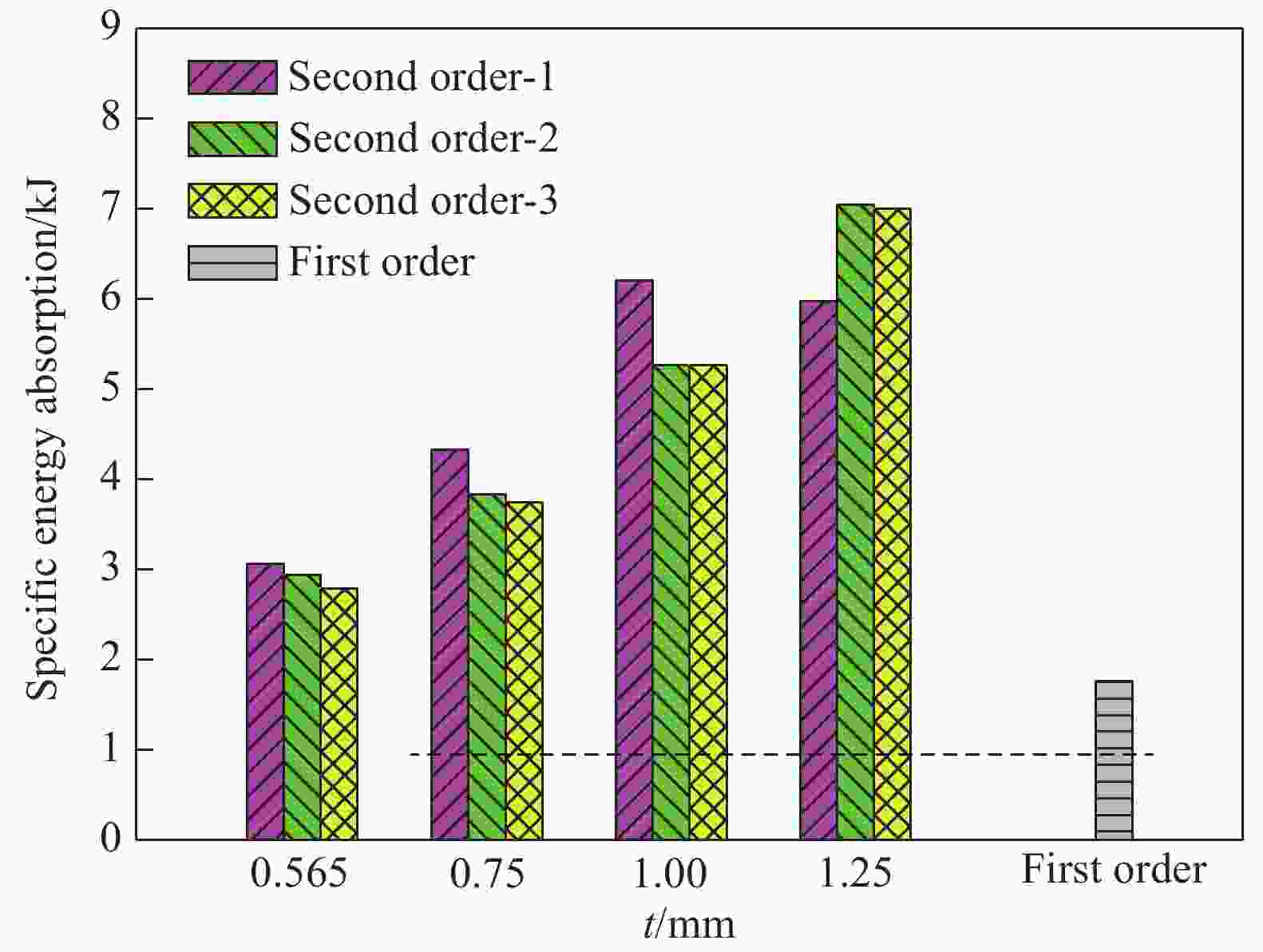
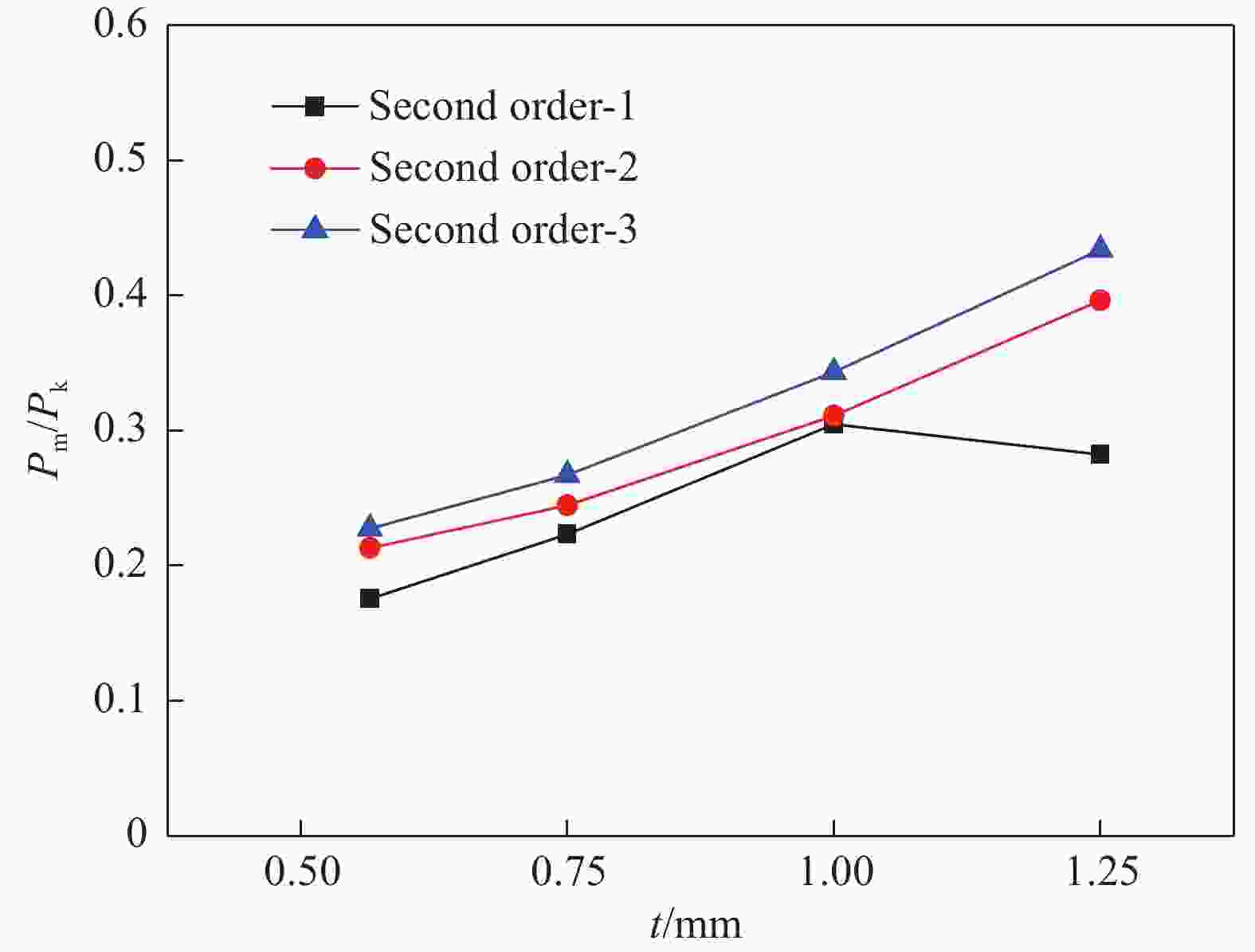
摘要: 采用数值模拟与理论分析相结合的方法研究了多层级波纹板夹芯结构在准静态压缩载荷下的变形规律与能量吸收性能,建立了结构临界失效载荷的计算公式,并与数值模拟结果进行了对比,理论预测与数值模拟结果吻合较好。分析了芯层厚度对二级芯层结构在压缩载荷下的变形模式及能量吸收性能的影响,并与一级结构进行了对比。结果表明:二级芯层结构的能量吸收性能显著优于一级芯层结构;随着结构芯层厚度增加,二级结构的比吸能和载荷效率增大;芯层厚度较小时二级单层结构的比吸能高于二级双层和三层结构,二级双层结构的比吸能略高于二级三层结构。Abstract: The deformation law and energy absorption performance of the multi-hierarchical sandwich structure under quasi-static compression have been studied by numerical and theoretical methods. The calculation formula of the critical failure load of the structure is established and compared with the numerical simulation results. The theoretical prediction is in good agreement with the numerical simulation results. Finite element models of the hierarchical corrugated core sandwich structure were established. The effects of core thickness on the deformation mode and energy absorption performance of secondary structure under quasi-static compression load were studied and compared with that of the primary structure.The results show that the energy absorption properties of the secondary core structure are significantly better than that of the primary core layer. As the thickness of the core increases, the specific energy absorption of the second order structure for single-layer is higher than that of the second order structure for two-layers and three-layers, and the specific energy absorption of the second order structure for two-layers is slightly higher than that of the second order structure for three-layers.
-
Key words:
- hierarchical structure /
- sandwich structure /
- energy absorption /
- numerical simulation
-
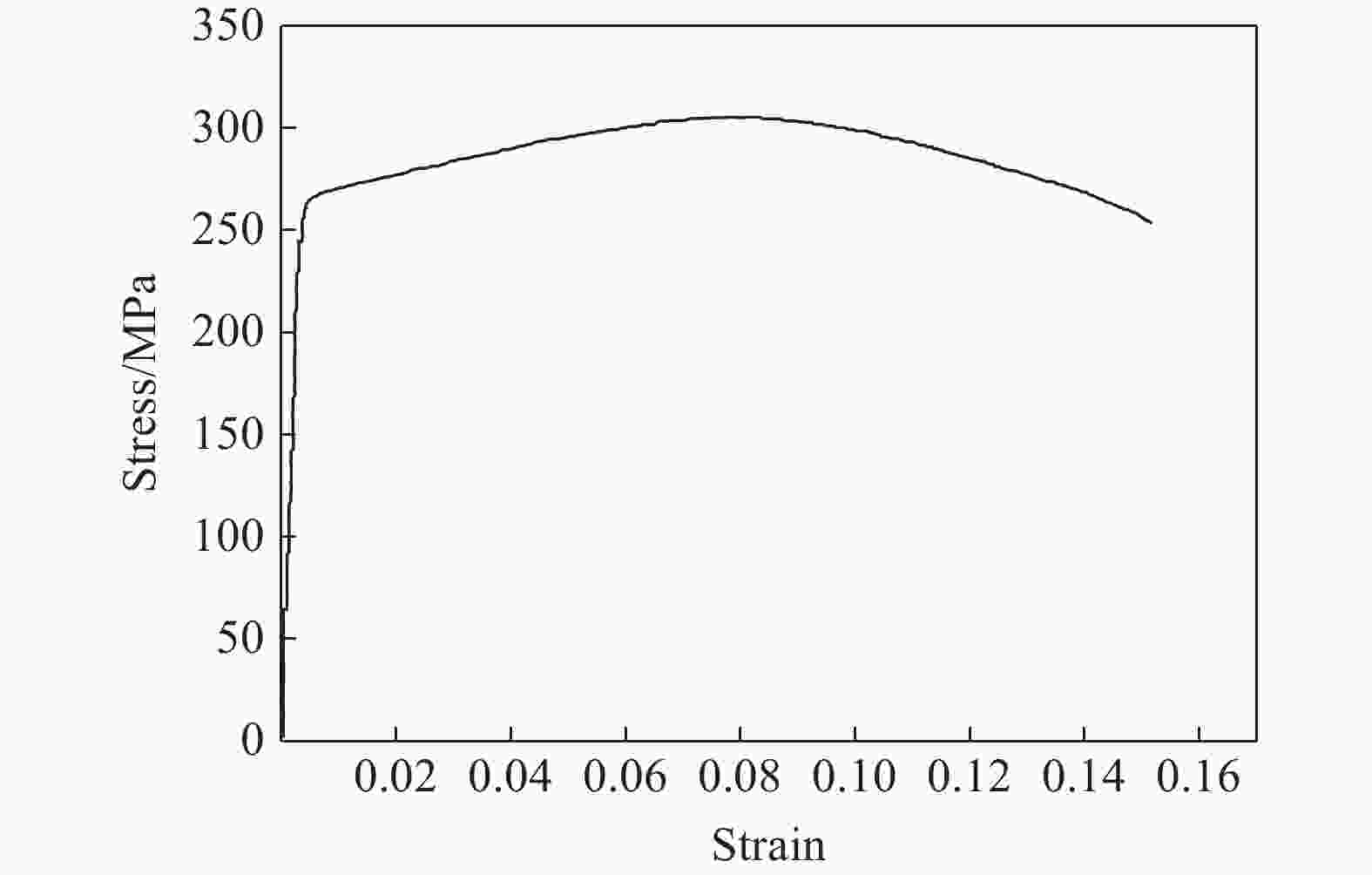
表 1 6061-T6铝合金材料性能
Table 1. Material properties of aluminum 6061-T6
Material ${\;\rho }$/(g·cm–3) ${{\sigma _{\rm{y}}}}$/MPa E/GPa ${\nu }$ Al 6061-T6 2.700 251 69 0.33 表 2 模型尺寸
Table 2. Size parameters of the model
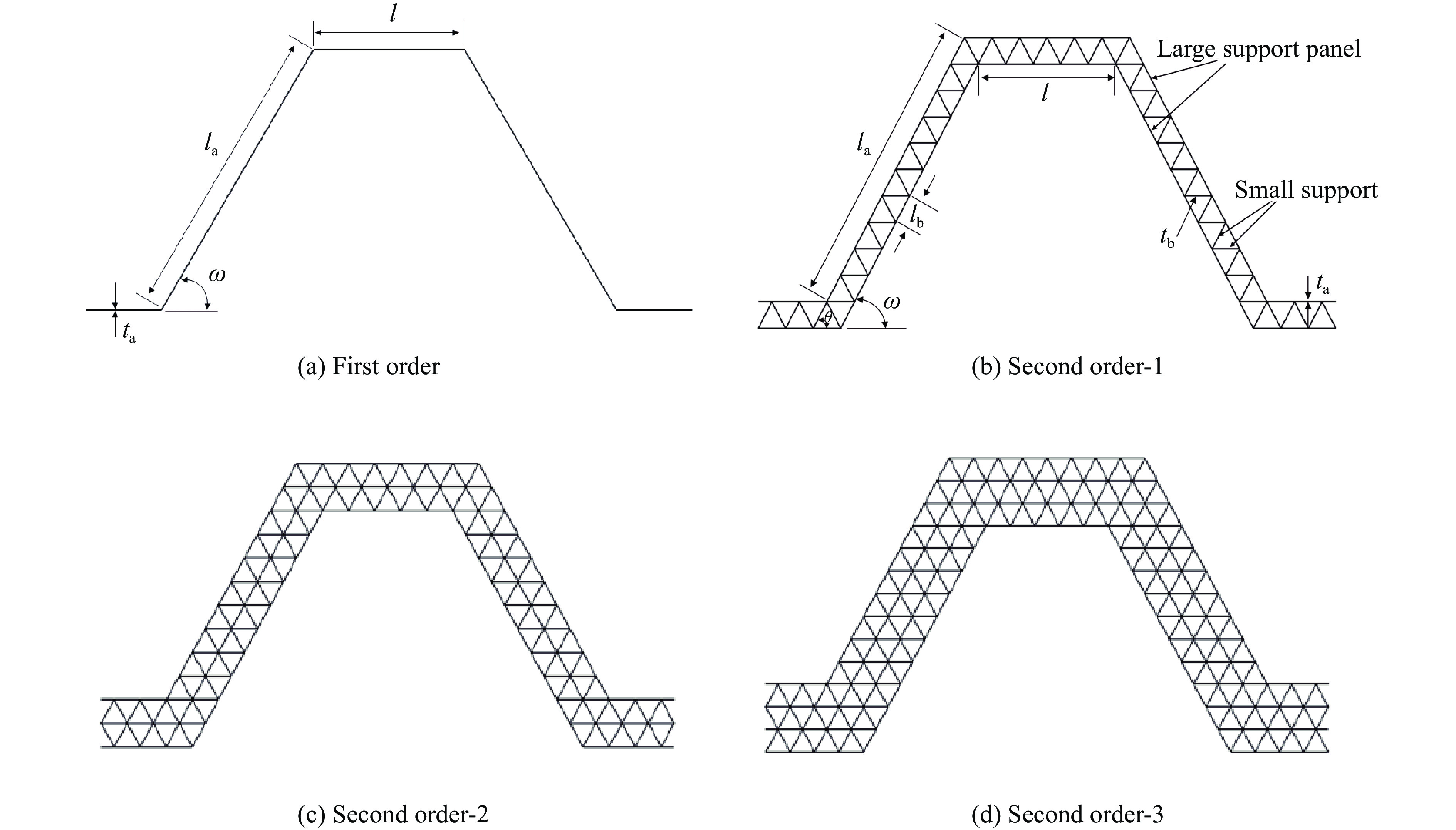
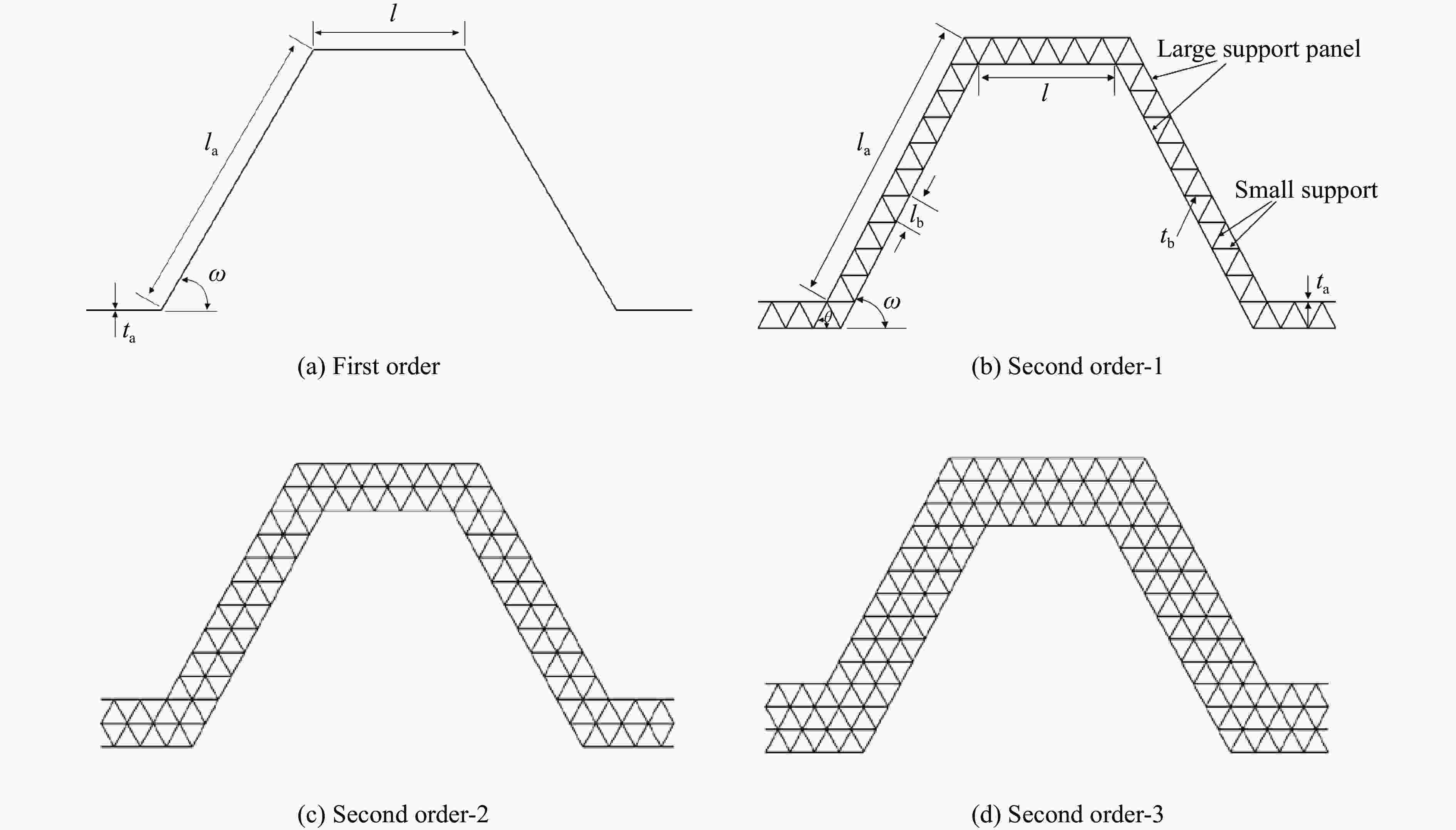
Type l/mm la/mm lb/mm ta/mm tb/mm ${ \theta }$/(°) ${ \omega }$/(°) First order 50 100 2 60 Second order-1 50 100 10 0.565/0.75/1.00/1.25 0.565/0.75/1.00/1.25 60 60 Second order-2 50 100 10 0.565/0.75/1.00/1.25 0.565/0.75/1.00/1.25 60 60 Second order-3 50 100 10 0.565/0.75/1.00/1.25 0.565/0.75/1.00/1.25 60 60 -
[1] LAKES R. Materials with structural hierarchy [J]. Nature, 1993, 361(6412): 511–515. doi: 10.1038/361511a0 [2] ZHANG J, SUPERNAK P, MUELLER-ALANDER S, et al. Improving the bending strength and energy absorption of corrugated sandwich composite structure [J]. Materials & Design, 2013, 52(24): 767–773. [3] HE W, LIU J, TAO B, et al. Experimental and numerical research on the low velocity impact behavior of hybrid corrugated core sandwich structures [J]. Composite Structures, 2016, 158: 30–43. doi: 10.1016/j.compstruct.2016.09.009 [4] HOU S, SHU C, ZHAO S, et al. Experimental and numerical studies on multi-layered corrugated sandwich panels under crushing loading [J]. Composite Structures, 2015, 126: 371–385. doi: 10.1016/j.compstruct.2015.02.039 [5] MEZA L R, ZELHOFER A J, CLARKE N, et al. Resilient 3D hierarchical architected metamaterials [J]. Proceedings of the National Academy of Sciences, 2015, 112(37): 11502–11507. doi: 10.1073/pnas.1509120112 [6] KOOISTRA G, DESHPANDE V, WADLEY H. Hierarchical corrugated core sandwich panel concepts [J]. Journal of Applied Mechanics, 2007, 74(2): 259–268. doi: 10.1115/1.2198243 [7] VELEA M N, SCHNEIDER C, LACHE S. Second order hierarchical sandwich structure made of self-reinforced polymers by means of a continuous folding process [J]. Materials & Design, 2016, 102: 313–320. [8] WU Q, GAO Y, WEI X, et al. Mechanical properties and failure mechanisms of sandwich panels with ultra-lightweight three-dimensional hierarchical lattice cores [J]. International Journal of Solids and Structures, 2017, s132/s133: 171–187. [9] WU Q, ASHKAN V, MOHAMAD E A, et al. Lattice materials with pyramidal hierarchy: systematic analysis and three dimensional failure mechanism maps [J]. Journal of the Mechanics and Physics of Solids, 2019, 125: 112–114. doi: 10.1016/j.jmps.2018.12.006 [10] LIU H, CHEN L, DU B, et al. Flatwise compression property of hierarchical thermoplastic composite square lattice [J]. Composite Structures, 2019, 210: 118–133. doi: 10.1016/j.compstruct.2018.11.047 [11] 王志华, 朱峰, 赵隆茂. 多孔金属夹芯结构动力学行为及其应用 [M]. 北京: 兵器工业出版社, 2010: 1–27.WANG Z H, ZHU F, ZHAO L M. Dynamic behavior and application of sandwich structures with cellular metal cores [M]. Beijing: The Publishing House of Ordnance Industry, 2010: 1–27. [12] JING L, WANG Z, ZHAO L. The dynamic response of sandwich panels with cellular metal cores to localized impulsive loading [J]. Composites Part B, 2016, 94: 52–63. doi: 10.1016/j.compositesb.2016.03.035 [13] CHEN Y, JIA Z, WANG L. Hierarchical honeycomb lattice metamaterials with improved thermal resistance and mechanical properties [J]. Composite Structures, 2016, 152: 395–402. doi: 10.1016/j.compstruct.2016.05.048 [14] CHEN Y, LI T, JIA Z, et al. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations [J]. Materials & Design, 2018, 137: 226–234. [15] YIN H, HUANG X, SCARPA F, et al. In-plane crashworthiness of bio-inspired hierarchical honeycombs [J]. Composite Structures, 2018, 192: 516–527. doi: 10.1016/j.compstruct.2018.03.050 [16] QIAO J, CHEN C. In-plane crushing of a hierarchical honeycomb [J]. International Journal of Solids & Structures, 2012, 85/86: 57–66. [17] 方耀楚. 二级层级褶皱结构力学性能研究与优化设计 [D]. 大连: 大连理工大学, 2014: 25–47.FANG Y C. Mechanical properties and optimal design of hierarchical corrugated structure with the second order [D]. Dalian: Dalian University of Technology, 2014: 25–47. [18] 田泽, 韩阳, 尹晓文, 等. 截面几何参数对帽型梁轴向冲击响应的影响 [J]. 高压物理学报, 2018, 32(5): 94–101. doi: 10.11858/gywlxb.20180521TIAN Z, HAN Y, YIN X W, et al. Effect of sectional geometrical parameters on axial impact responses of hat-section beam [J]. Chinese Journal of High Pressure Physics, 2018, 32(5): 94–101. doi: 10.11858/gywlxb.20180521 [19] SANTOSA S P, WIERZBICKI T. Experimental and numerical studies of foam-filled sections [J]. International Journal of Impact Engineering, 2000, 24(5): 509–534. doi: 10.1016/S0734-743X(99)00036-6 [20] 宋宏伟, 范子杰, 虞钢. 几类典型耐撞性结构吸能性能的比较[C]//2004汽车安全技术国际研讨会暨汽车安全技术学术年会, 2004. -






 下载:
下载: