Numerical Simulation of Thin Steel Target Perforated by Conical-Nosed Projectile with Yaw Angle
-
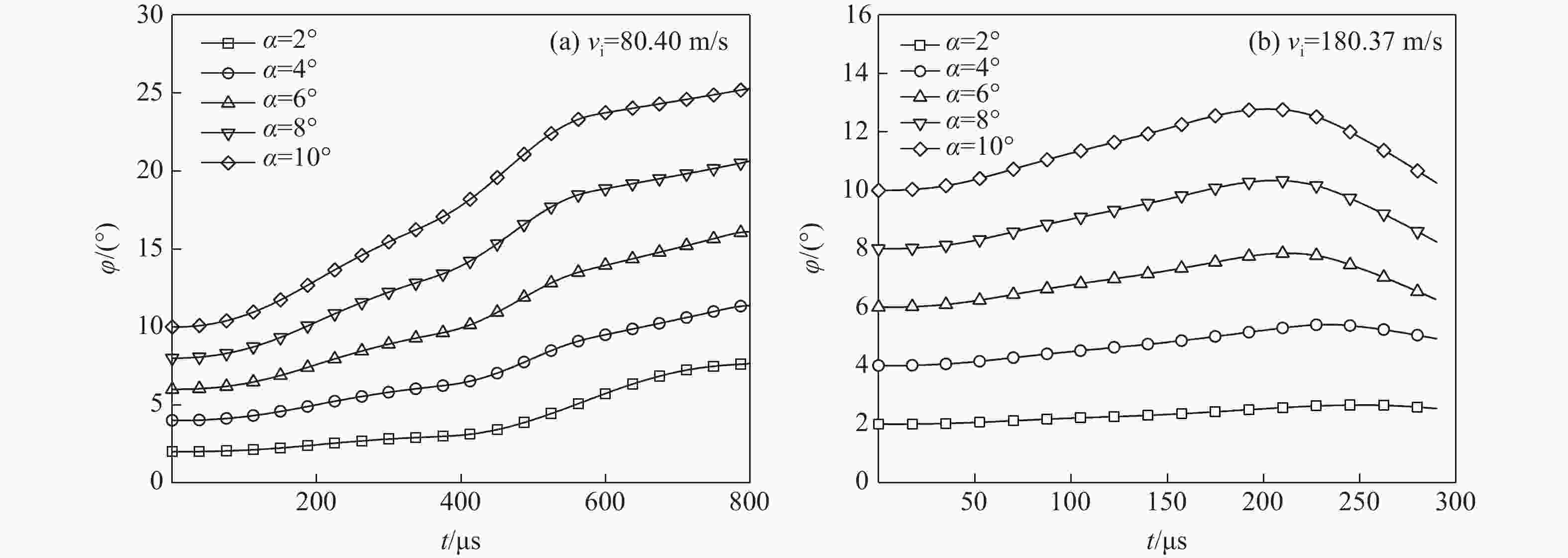
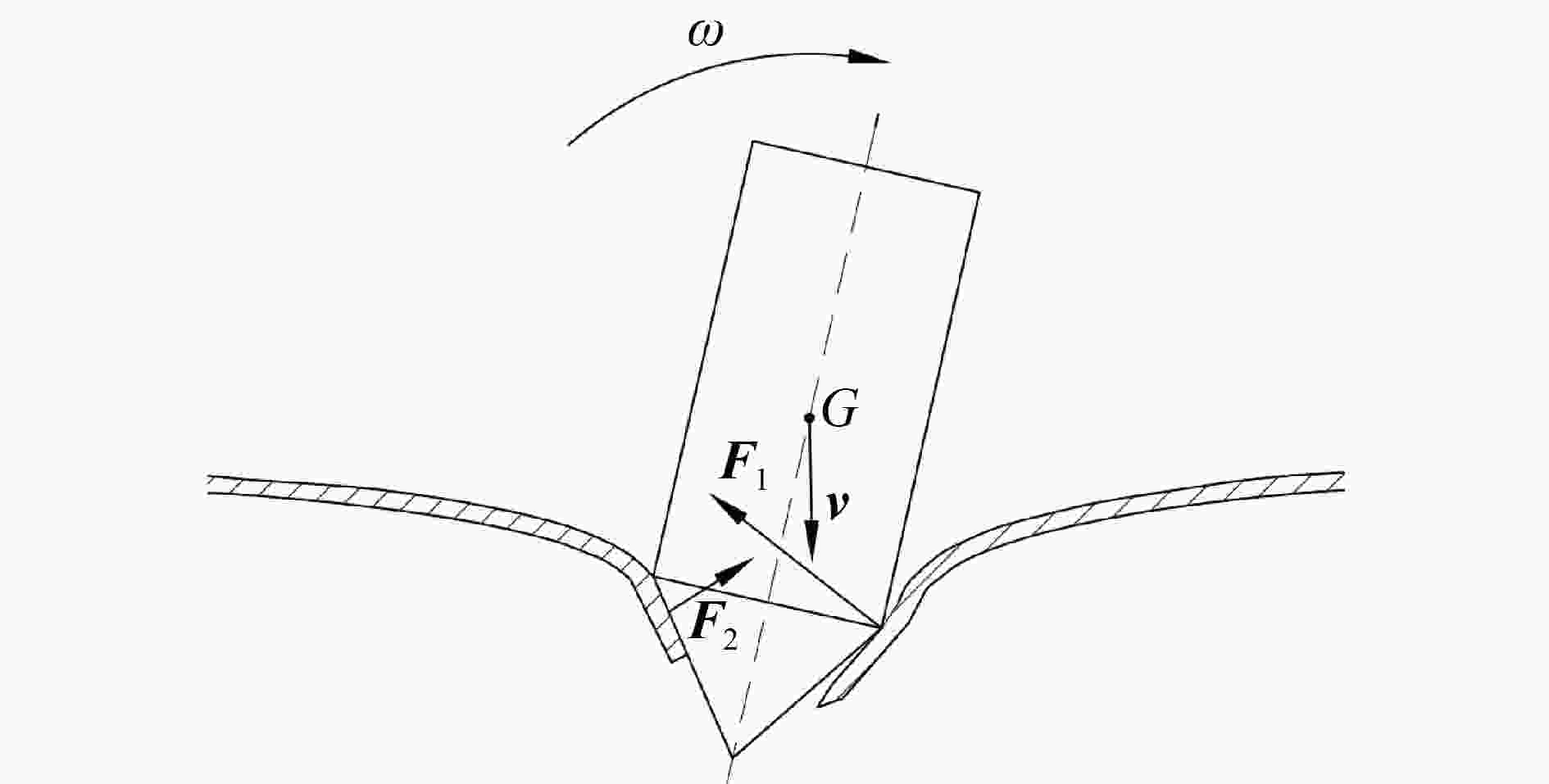
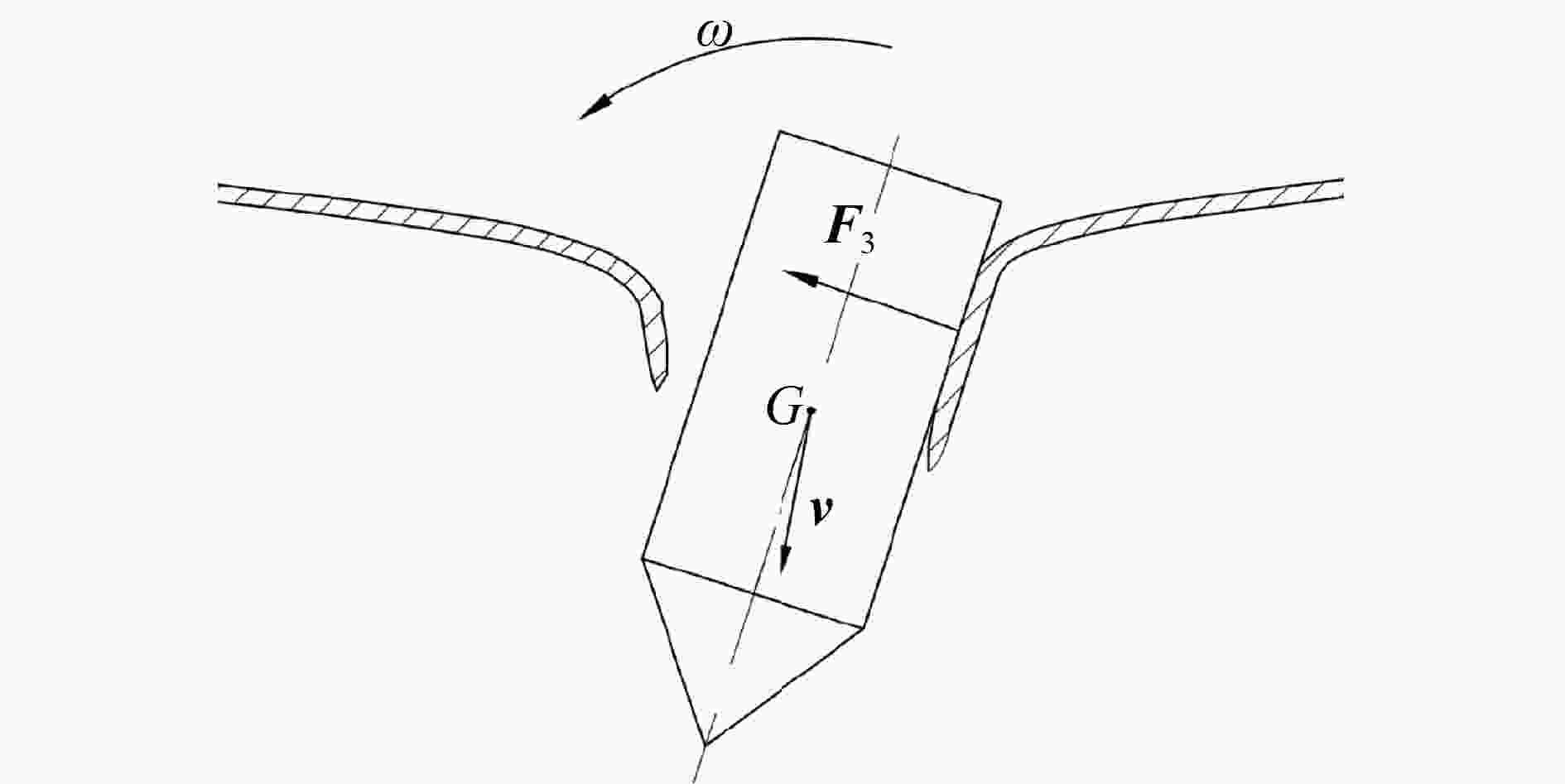
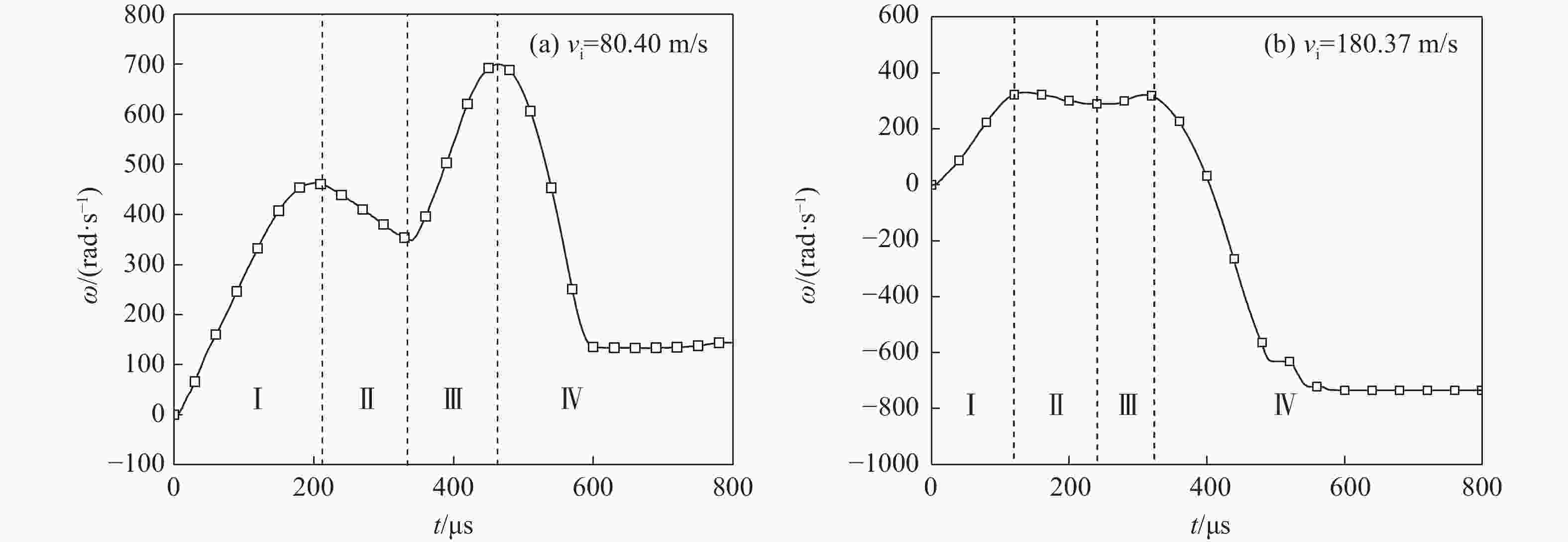
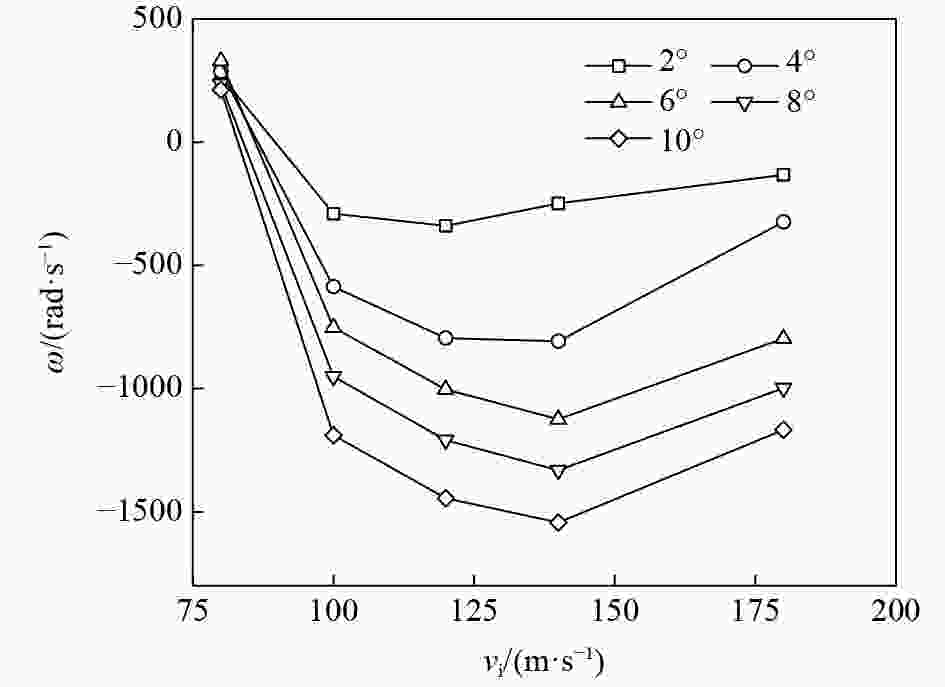
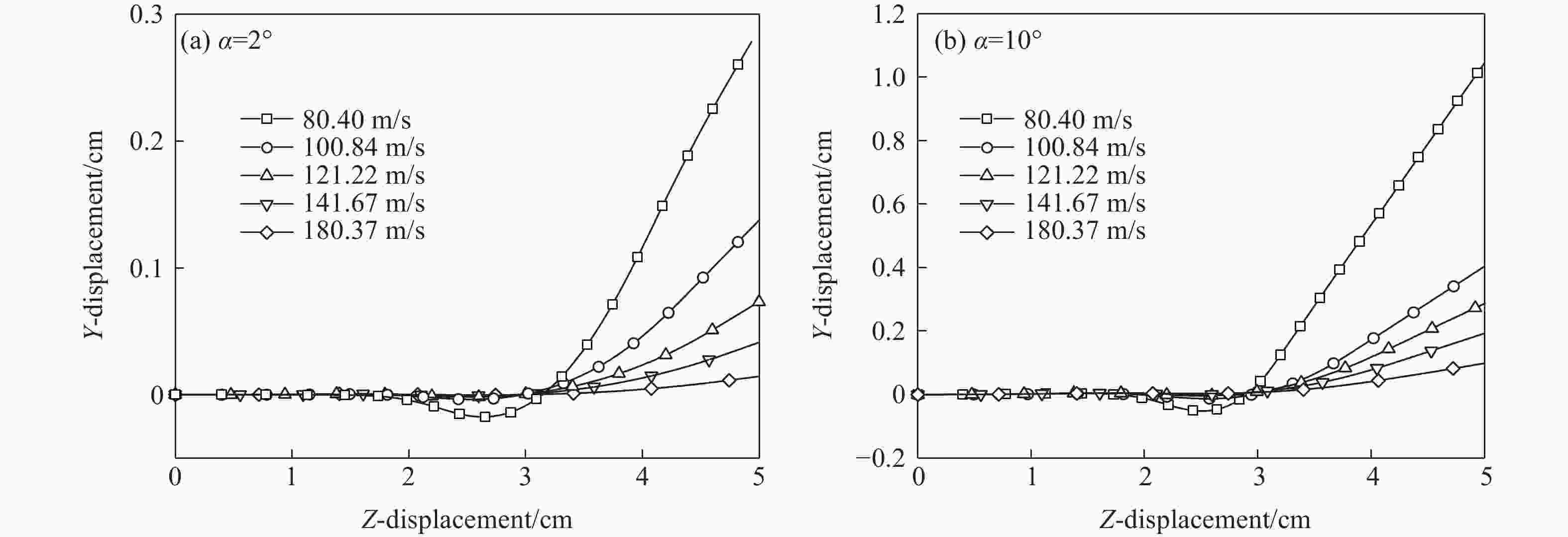
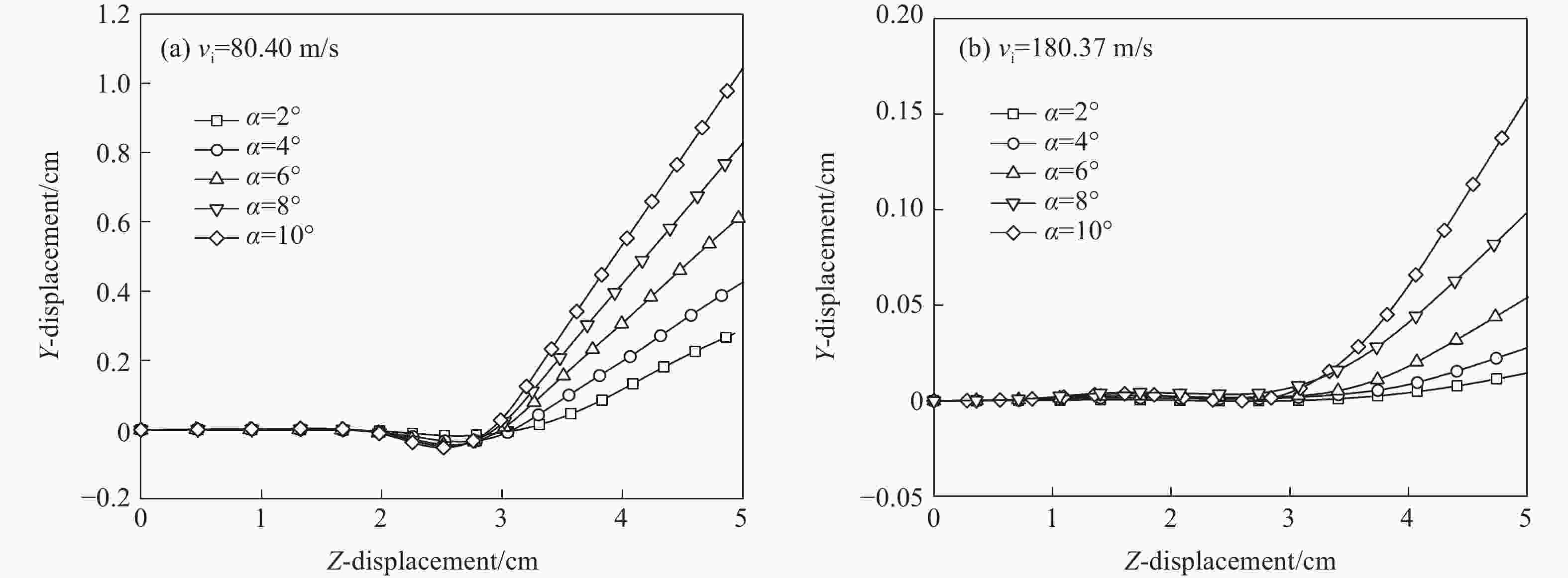
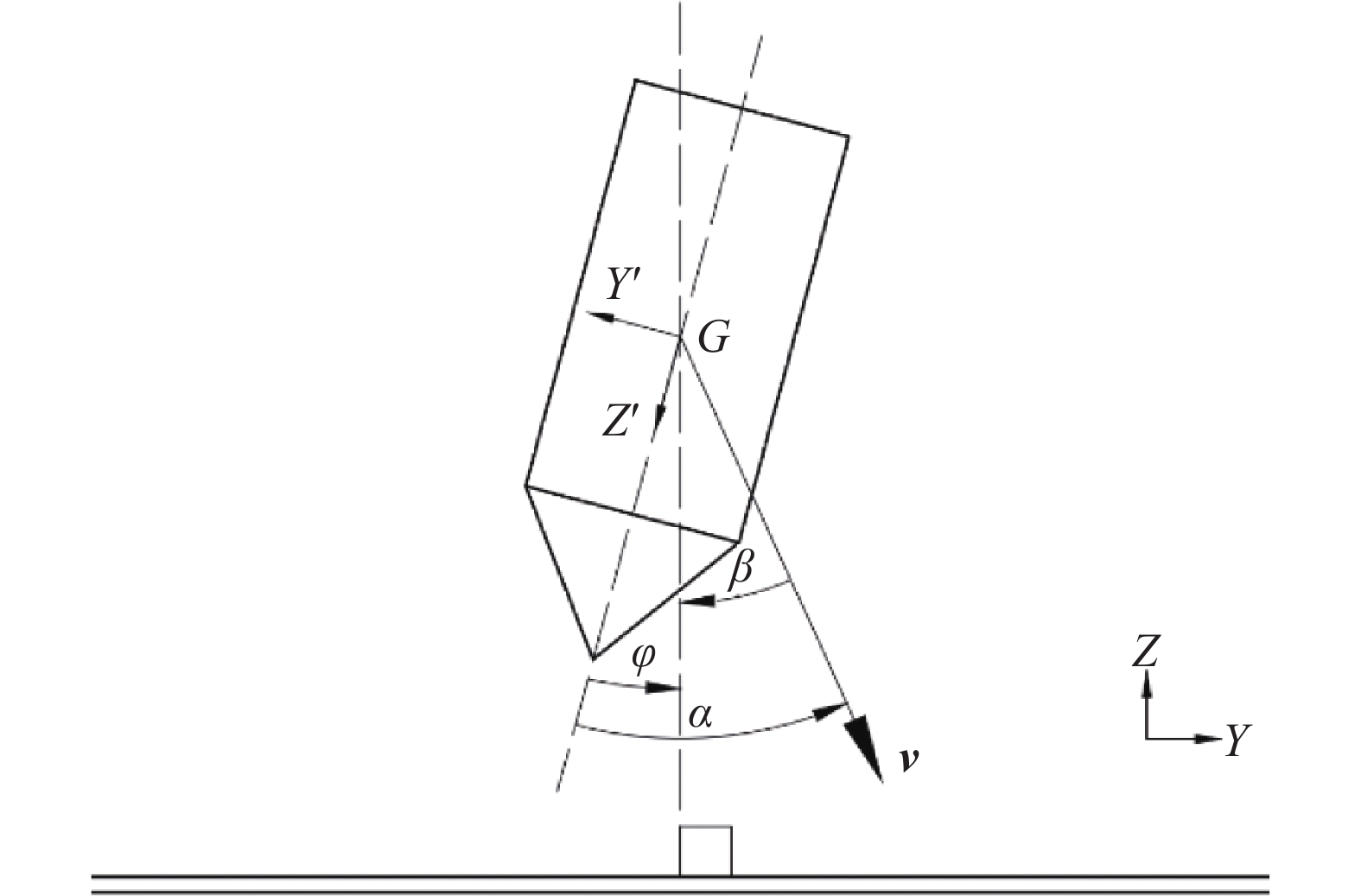
摘要: 为了研究攻角对锥头弹体贯穿薄钢靶破坏模式和弹体偏转的影响,利用ANSYS/LS-DYNA有限元软件建立了锥头弹体以2°~10°攻角贯穿薄钢靶的模型。先验证了模型及参数的可靠性,在此基础上进行了锥头弹体在不同攻角和初始速度条件下的贯穿数值模拟。结合靶板的破坏与弹体的偏转过程提出了一种四阶段分析模型,并系统地研究了攻角对弹道和弹体偏转角变化规律的影响。结果表明:攻角贯穿薄钢靶失效模式为非对称花瓣形破坏;攻角越大,初始速度越小(大于弹道极限速度),弹道偏转越明显;弹体偏转角变化规律与初始速度范围相关,当初始速度高于1.4倍弹道极限时,弹体偏转角呈现先增大后减小的变化趋势;弹体出靶时刻的角速度随攻角的增大而增大,随着初始速度的增加先反向增大后减小。Abstract: Numerical simulations are conducted for perforation of conical projectile impacting on thin steel target with various yaw angles to investigate the influence of yaw angle. The finite element models of conical projectile impacting on thin steel target with yaw angle varying from 2° to 10° are established with the non-linear finite element code ANSYS/LS-DYNA. After the reliability of numerical simulations is verified, numerical simulations of conical projectile impacting on thin steel target with different yaw angles and initial velocities are carried out. A four-step model to analyze the process of projectile’s deflection is addressed by comparing the process of target’s failure and projectile’s deflection. At last, we discuss the projectile’s trajectory angel deflection and angular velocity through the validated numerical analysis. The results show that the failure of asymmetric petalling occurs when a thin plate is impacted by conical-nosed projectile with yaw angle. With the increase of the yaw angle and the decrease of initial velocity, the deflection of the trajectory will be more obvious; the deflection change of projectile relates to the initial velocity; the deflection angle shows a trend of increasing first and subsequently decreasing when the initial impact velocity is relatively high (greater than about 1.4 times the ballistic limit). When the projectile moves out of target, the angular velocity rises with the increase of the yaw angle, but it increases reversely and then reduces with the increase of initial velocity.
-
Key words:
- conical-nosed projectiles /
- yaw angle /
- perforation /
- attitude deflection /
- finite element simulation
-
A/MPa B/MPa n c ${\dot \varepsilon _0}$/s–1 Tr/K Tmelt/K 154 464 0.37 0.02 0.0001 300 1600 m D1 D2 D3 D4 D5 $\chi $ 0.7 1.2 0 0 0 0 0.9 $\rho $/(g·cm–3) C0/(m·s–1) S1 ${\gamma _0}$ $a$ cp/(J·kg–1· K–1) 7.80 4578 1.33 1.67 0.47 470 表 2 弹体正撞击靶板的初始与剩余速度
Table 2. Initial and residual velocities of the projectile impacting target vertically
vi/(m·s–1) vr/(m·s–1) Experiment results[13] Simulation results 72.32 0.43 6.81 80.40 37.09 42.28 100.84 67.13 75.84 121.22 92.37 101.26 141.67 118.10 124.77 180.37 156.24 160.99 表 3 模型参数及弹道极限
Table 3. Model parameters and ballistic limits
Method a q vbl/(m·s–1) Experiment 1.00 1.95 72.85 Numerical simulation 1.00 2.20 72.13 -
[1] BACKMAN M E, GOLDSMITH W. The mechanics of penetration of projectiles into targets [J]. International Journal of Engineering Science, 1978, 16(1): 1–99. doi: 10.1016/0020-7225(78)90002-2 [2] CORBETT G G, REID S R, JOHNSON W. Impact loading of plates and shells by free-flying projectiles: a review [J]. International Journal of Impact Engineering, 1996, 18(2): 141–230. doi: 10.1016/0734-743X(95)00023-4 [3] ZUKAS J A. Impact dynamics [M].New York:Wiley,1982. [4] ANDERSON C E JR, BODNER S R. Ballistic impact: the status of analytical and numerical modeling [J]. International Journal of Impact Engineering, 1988, 7(1): 9–35. doi: 10.1016/0734-743X(88)90010-3 [5] 钱伟长. 穿甲力学 [M]. 北京: 国防工业出版社, 1984.QIAN W C. Mechanics of perforation [M]. Beijing: National Defense Industry Press, 1984. [6] GOLDSMITH W. Non-ideal projectile impact on targets [J]. International Journal of Impact Engineering, 1999, 22(2/3): 95–395. [7] DENG Y F, LI J F, JIA B H, et al. Numerical study of failure modes and crack propagation in 2A12 aluminum target against blunt-nosed projectile at low yaw angle [J]. Strength of Materials, 2016, 48(6): 834–849. doi: 10.1007/s11223-017-9830-3 [8] 徐双喜, 吴卫国, 李晓彬, 等. 锥头弹小斜角侵彻薄板剩余速度理论分析 [J]. 弹道学报, 2010, 22(3): 58–62.XU S X, WU W G, LI X B, et al. Theoretical analysis on residual velocity of conical projectile after penetrating thin plate at low oblique angle [J]. Journal of Ballistics, 2010, 22(3): 58–62. [9] 熊飞, 石全, 张成, 等. 不同头部形状半穿甲战斗部侵彻薄钢板数值模拟 [J]. 弹箭与制导学报, 2015(1): 55–58.XIONG F, SHI Q, ZHANG C, et al. Numerical simulation on the semi-armor-piercing warhead with different nose shapes penetrating thin steel target [J]. Journal of Projectiles, Rockets, Missile and Guidance, 2015(1): 55–58. [10] 董三强, 蔡星会, 王国亮, 等. 攻角对半穿甲战斗部侵彻航母双层靶板的效应研究 [J]. 舰船科学技术, 2017(21): 37–41.DONG S Q, CAI X H, WANG G L, et al. Numerical simulation research on effect of warhead penetrating double-layer aircraft carrier targets [J]. Ship Science and Technology, 2017(21): 37–41. [11] 侯旷怡, 李可达, 张新伟. 着靶姿态对半穿甲战斗部穿甲过程的影响 [J]. 兵器装备工程学报, 2017(4): 65–68.HOU K Y, LI K D, ZHANG X W. Influence of hitting attitude in armor-piercing process [J]. Journal of Ordnance Equipment Engineering, 2017(4): 65–68. [12] 邓云飞, 袁家俊. 攻角对卵形头弹撞击铝合金薄板影响的数值研究 [J]. 高压物理学报, 2018, 32(4): 045102. doi: 10.11858/gywlxb.20170601DENG Y F, YUAN J J. Numerical research of influence of attack angle on thin aluminum alloy plate impacted by ogival-nosed projectile [J]. Chinese Journal of High Pressure Physics, 2018, 32(4): 045102. doi: 10.11858/gywlxb.20170601 [13] KPENYIGBA K M, JANKOWIAK T, RUSINEK A, et al. Influence of projectile shape on dynamic behavior of steel sheet subjected to impact and perforation [J]. Thin-Walled Structures, 2013, 65: 93–104. doi: 10.1016/j.tws.2013.01.003 [14] RECHT R F, IPSON T W. Ballistic perforation dynamics [J]. Journal of Applied Mechanics, 1963, 30(3): 384. doi: 10.1115/1.3636566 -






 下载:
下载: