Dynamic Compaction Behaviors of Copper Powders Using Multi-Particle Finite Element Method
-
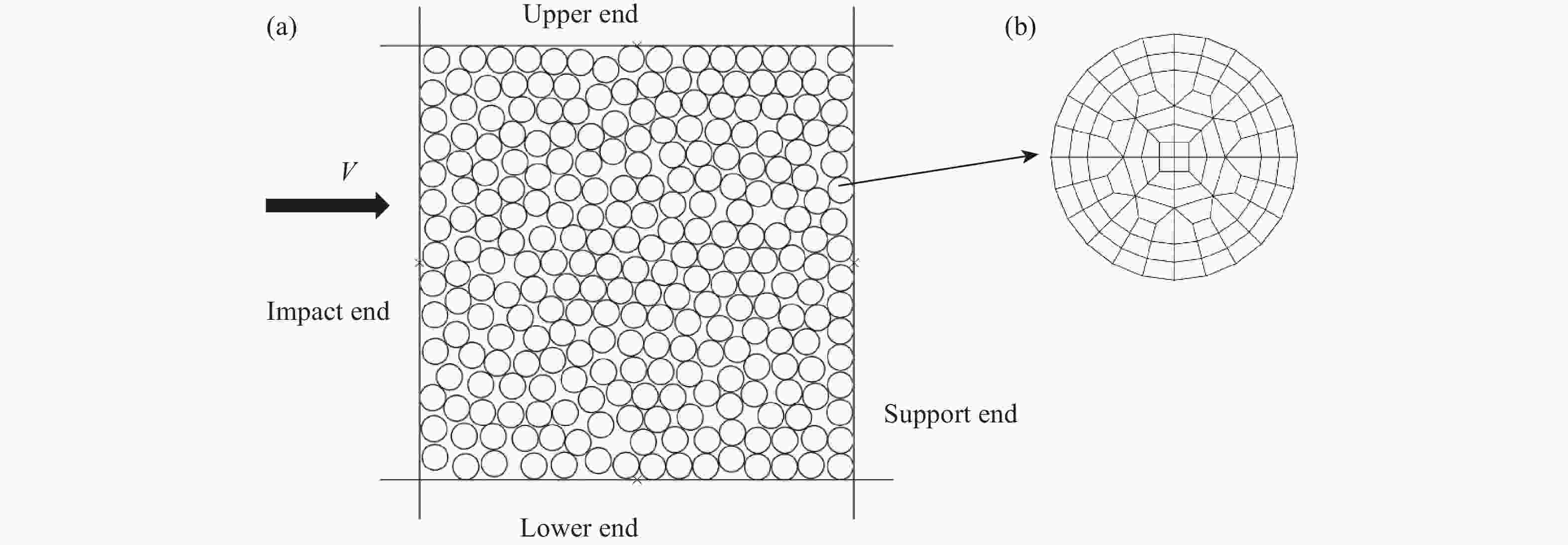
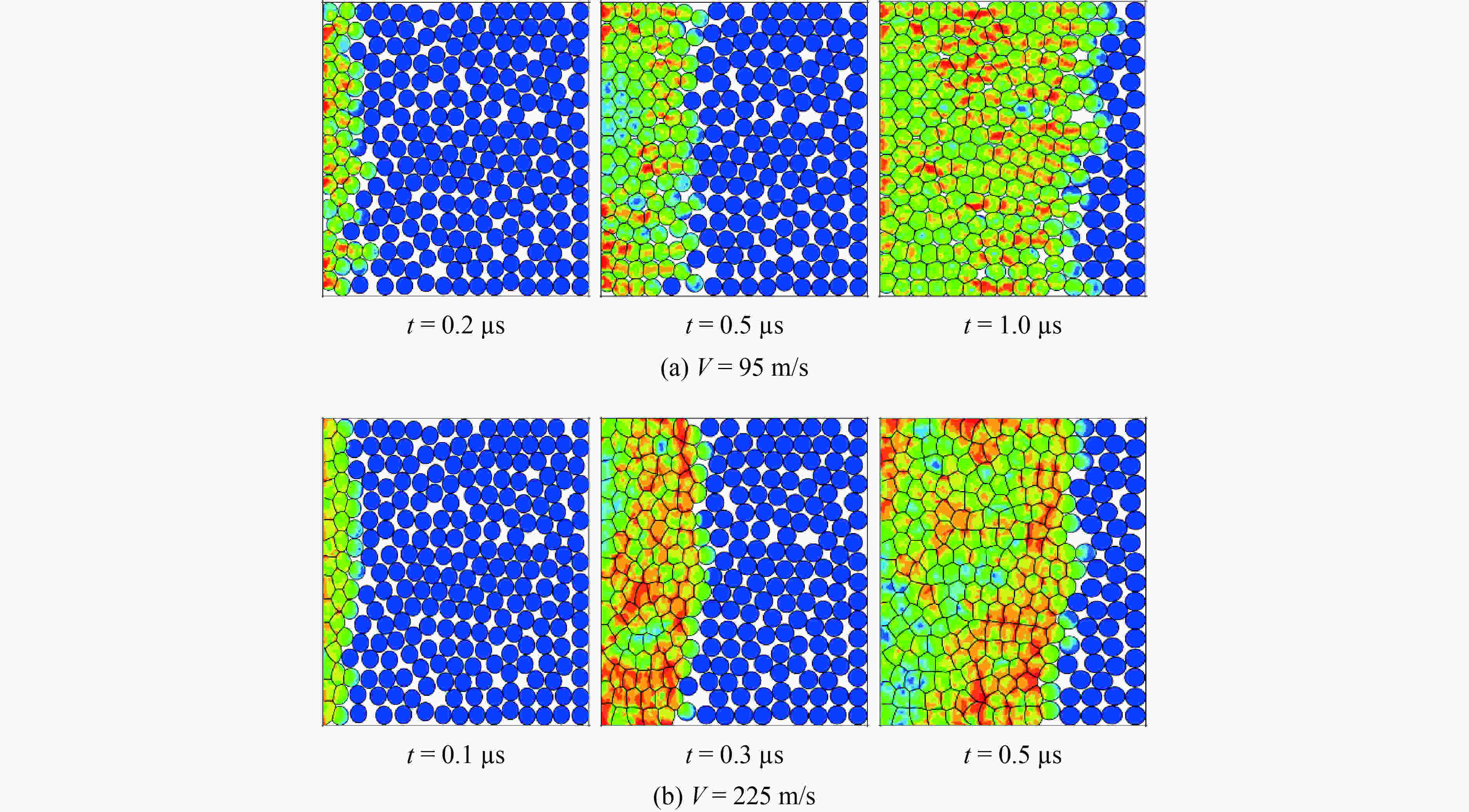
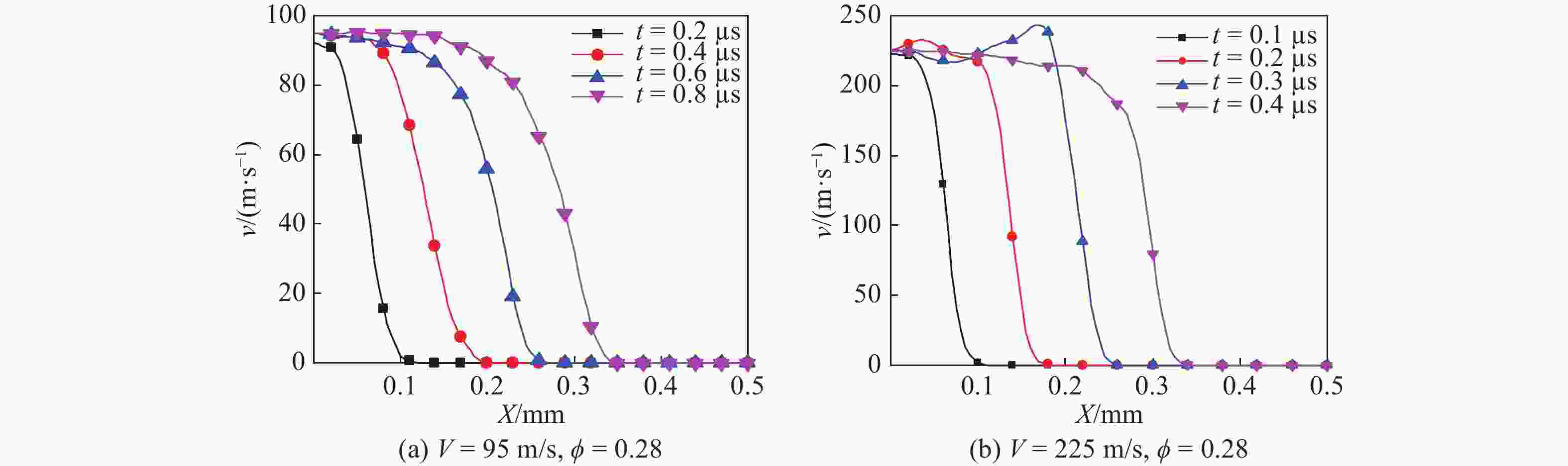
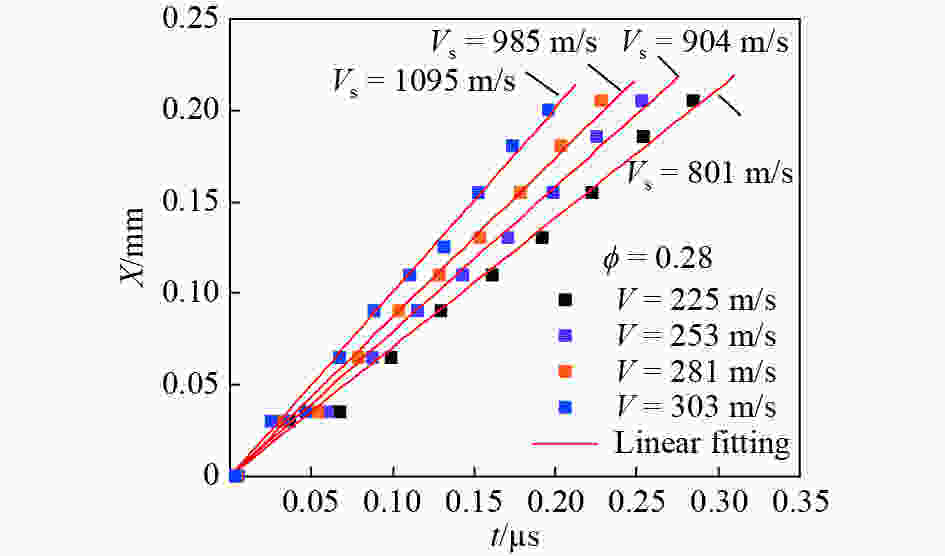
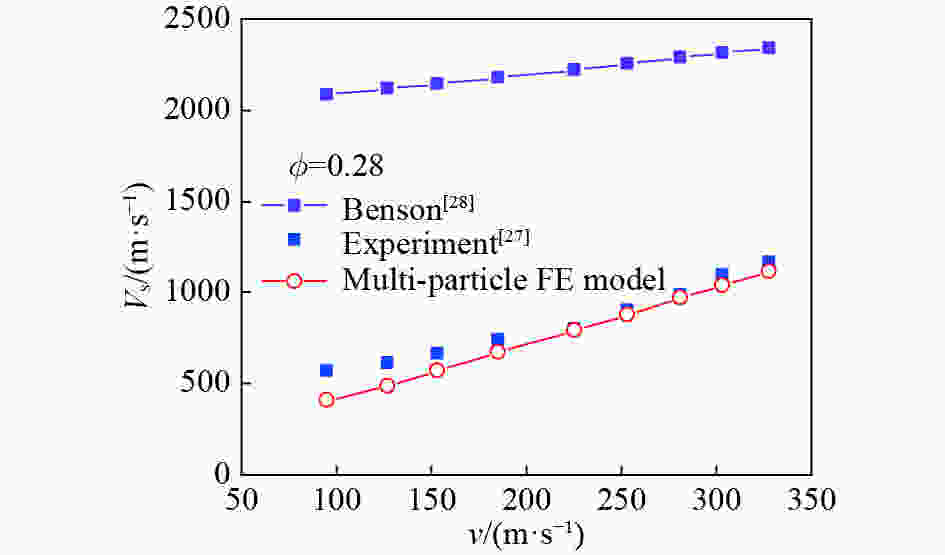
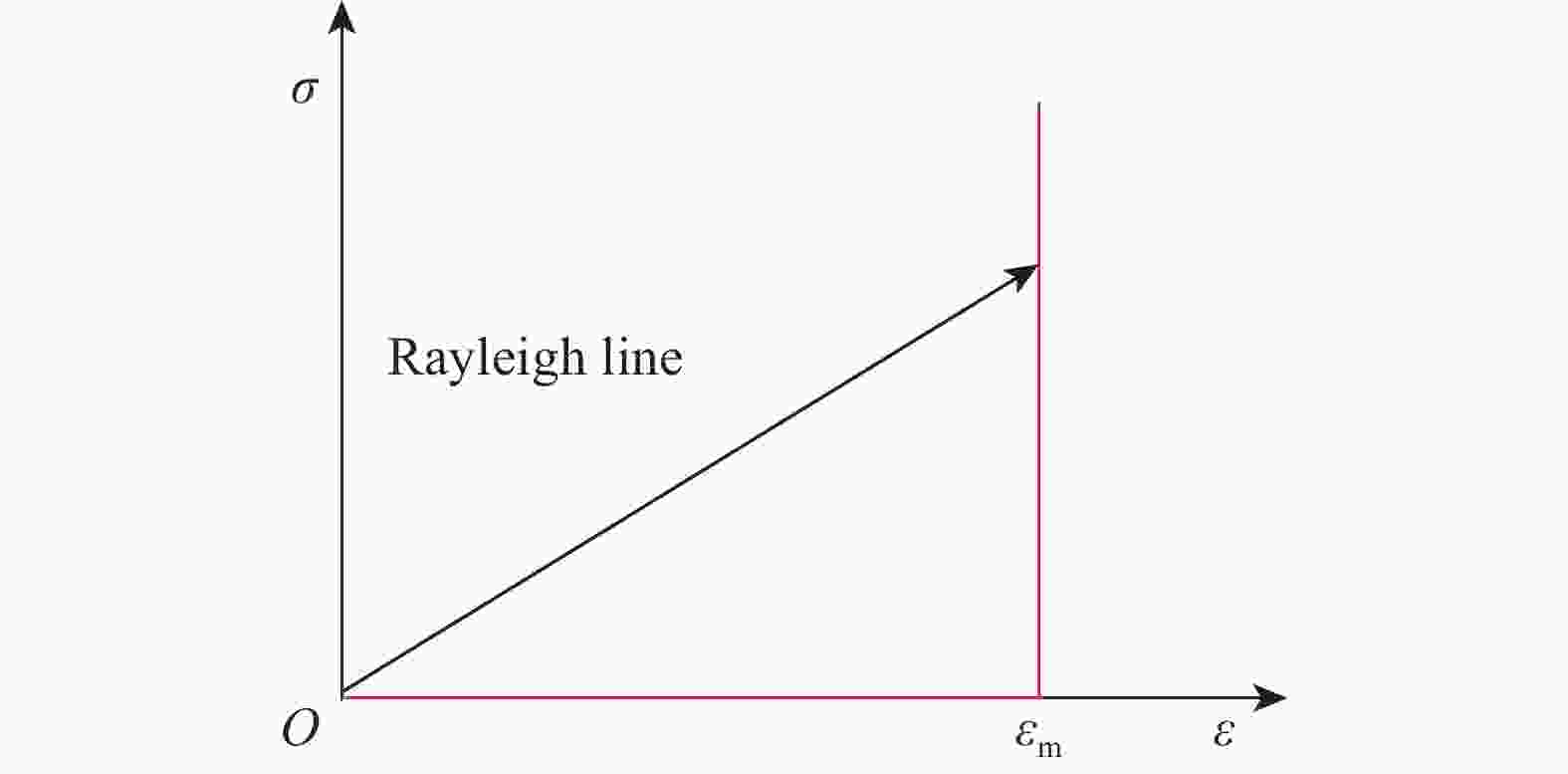
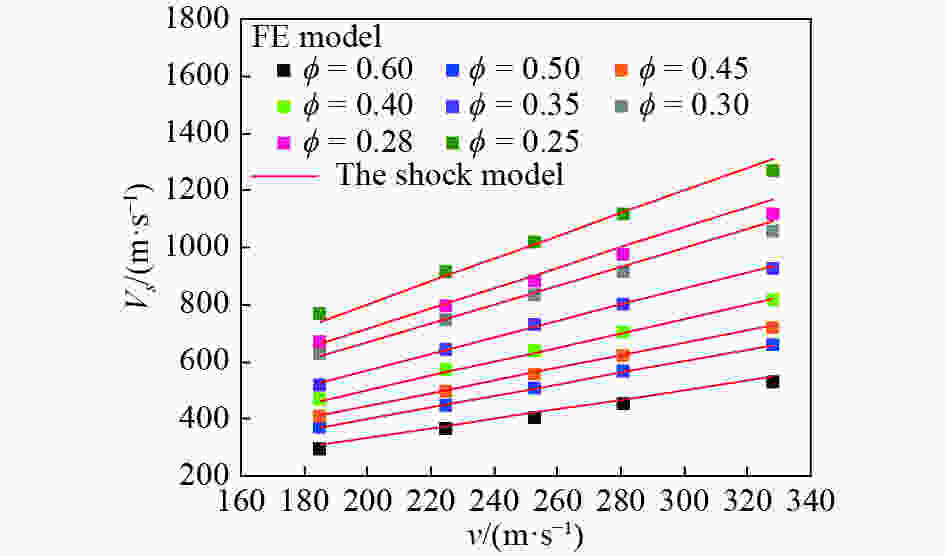
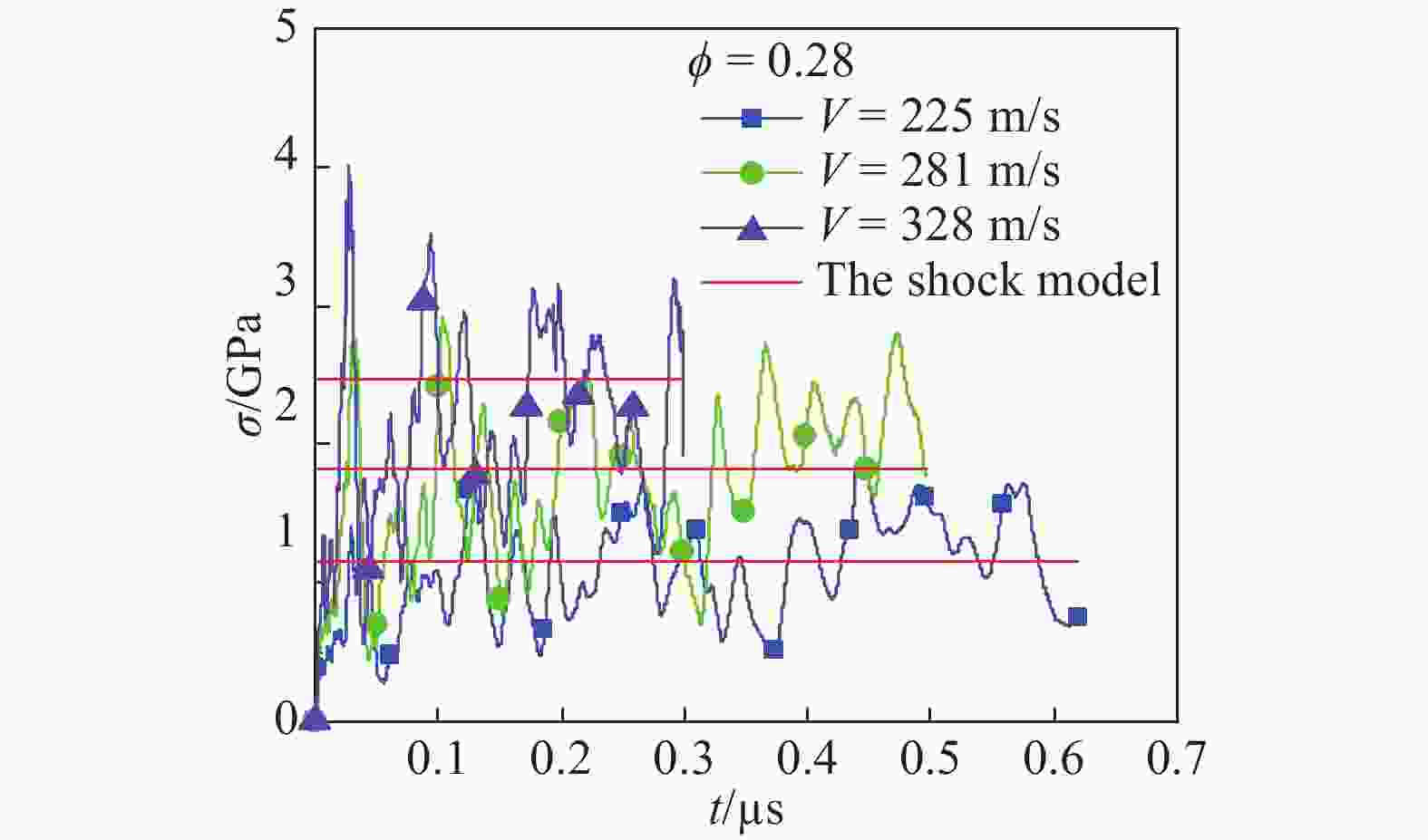
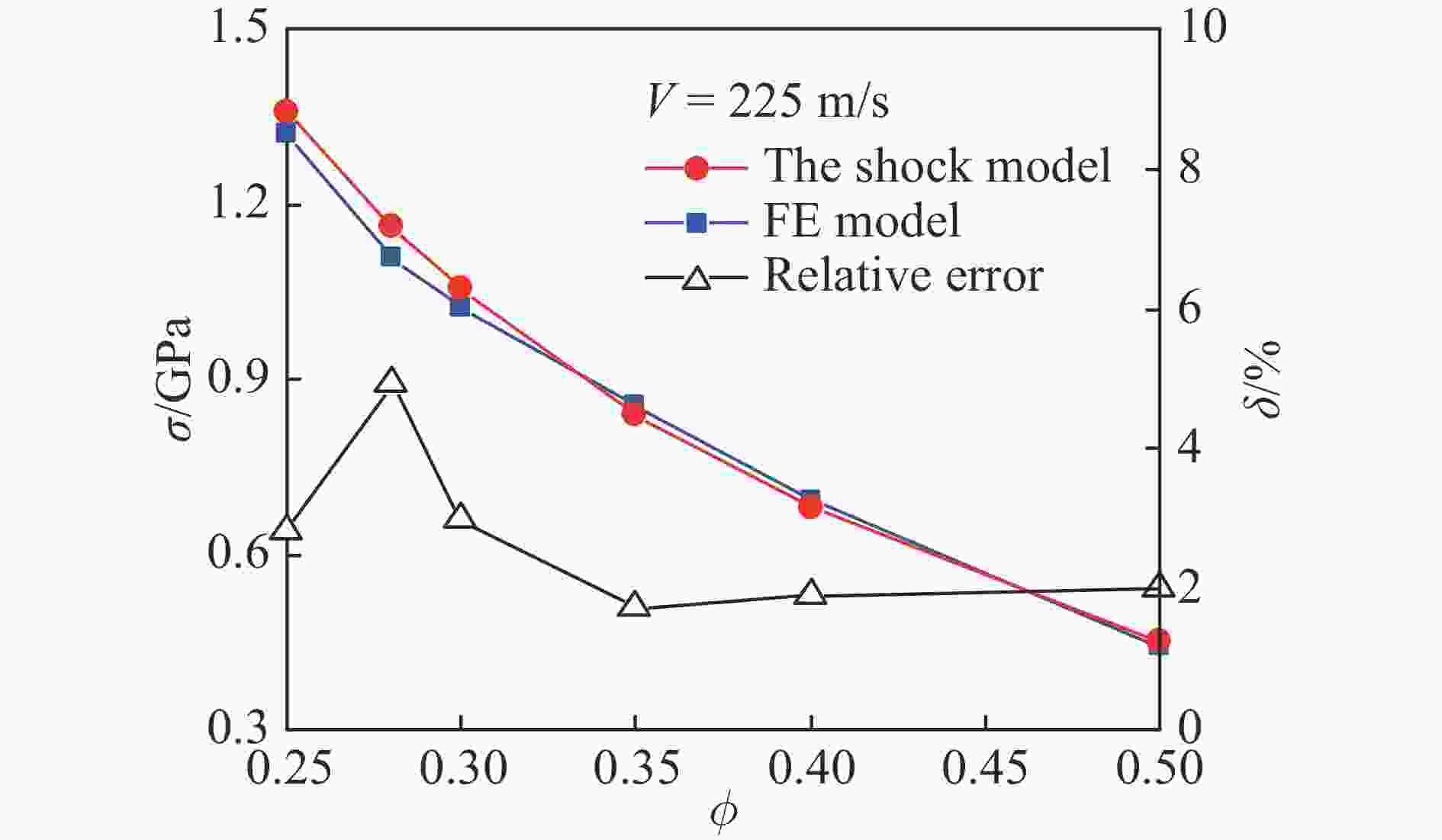
摘要: 颗粒金属材料的宏观力学性能与其细观特性密切相关,金属粉末的冲击压缩问题有待深入研究。选用实验结果较为丰富的铜粉末作为研究对象,基于多颗粒有限元法建立了颗粒金属材料的二维数值分析模型,研究了铜粉末在冲击压缩下的力学行为。数值计算结果表明,在较高速度冲击下颗粒金属材料呈现出高度局部化的变形带,变形带如同冲击波一样从冲击端向支撑端传播。利用速度场计算方法,计算得到了塑性冲击波波阵面的位置,进而获得了不同孔隙率(0.25~0.60)铜粉末的粒子速度与冲击波波速之间的Hugoniot关系,其在较高冲击速度(200~300 m/s)下与实验结果吻合较好。发展了以动态锁定应变为唯一参数的冲击波模型,较好地表征了铜粉末在较高速度冲击下的Hugoniot关系和波后应力。
-
关键词:
- 颗粒金属材料 /
- 冲击压缩 /
- 多颗粒有限元法 /
- 冲击波模型 /
- Hugoniot关系
Abstract: The meso-scale characteristics of granular metal materials play an important role in macroscopic mechanical behavior. The dynamic compression behavior of metal powders still needs further researches. In this paper, the copper powders persisting rich experimental results were selected as the research objects. Based on the multi-particle finite element method, a two-dimensional numerical analysis model of granular metal materials was established, and the mechanical behavior of copper powders under impact compression was studied. The numerical results show that the granular metal materials exhibit a highly localized deformation band under high velocity impact, and the deformation bands propagate from the impact end to the support end like a shock wave. By using the velocity field calculation method, the position of the plastic impact wave front was calculated, and the Hugoniot relationship between the particle velocity and the shock wave velocity of copper powders with different porosities (0.25–0.60) was obtained. The numerical results agree well with the experimental results at high impact velocities (200–300 m/s). The shock wave model using the dynamic locking strain as the only parameter was developed. It is found that the Hugoniot relationship and the stress behind the shock wave front of the copper powders under high velocity impact are well characterized. -
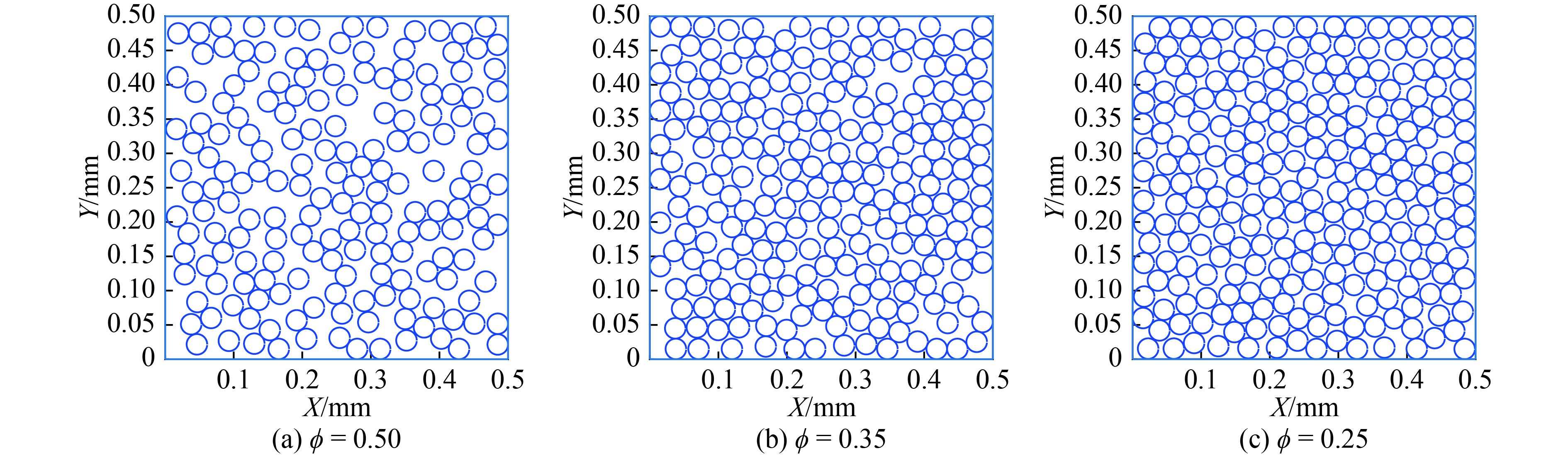
表 1 不同孔隙率下细观模型所含颗粒数
Table 1. Particle numbers of mesoscale model at different porosities
Porosity ($\phi $) Number of particles (N) 0.60 142 0.50 177 0.45 195 0.40 213 0.35 230 0.30 248 0.28 255 0.25 265 -
[1] KELLY A, ZWEBEN C. Comprehensive composite materials [J]. Materials Today, 1999, 2(1): 20–21. doi: 10.1016/S1369-7021(99)80033-9 [2] CLYNE T W, WITHERS P J. An introduction to metal matrix composites [M]. New York, NY, USA: Cambridge University Press, 1993, 1(1): 155–164. [3] KONDO K I, SOGA S, SAWAOKA A, et al. Shock compaction of silicon carbide powder [J]. Journal of Materials Science, 1985, 20(3): 1033–1048. doi: 10.1007/BF00585748 [4] MORRIS D G. Bonding processes during the dynamic compaction of metallic powders [J]. Materials Science & Engineering, 1983, 57(2): 187–195. [5] SHAO B, LIU Z, ZHANG X. Explosive consolidation of amorphous cobalt-based alloys [J]. Journal of Materials Processing Technology, 1999, 85(1/2/3): 121–124. [6] CARROLL M M, HOLT A C. Static and dynamic pore-collapse relations for ductile porous materials [J]. Journal of Applied Physics, 1972, 43(4): 1626–1636. doi: 10.1063/1.1661372 [7] BUTCHER B M, CARROLL M M, HOLT A C. Shock-wave compaction of porous aluminum [J]. Journal of Applied Physics, 1974, 45(9): 3864–3875. doi: 10.1063/1.1663877 [8] BOADE R R. Dynamic compression of porous tungsten [J]. Journal of Applied Physics, 1969, 40(9): 3781–3785. doi: 10.1063/1.1658272 [9] THADHANI N N, GRAHAM R A, ROYAL T, et al. Shock-induced chemical reactions in titanium-silicon powder mixtures of different morphologies: time-resolved pressure measurements and materials analysis [J]. Journal of Applied Physics, 1997, 82(3): 1113–1128. doi: 10.1063/1.365878 [10] BOSLOUGH M B. A thermochemical model for shock-induced reactions (heat detonations) in solids [J]. Journal of Chemical Physics, 1990, 92(3): 1839–1848. doi: 10.1063/1.458066 [11] NIEH T G, LUO P, NELLIS W, et al. Dynamic compaction of aluminum nanocrystals [J]. Acta Materialia, 1996, 44(9): 3781–3788. doi: 10.1016/1359-6454(96)83816-X [12] BENSON D J. An analysis by direct numerical simulation of the effects of particle morphology on the shock compaction of copper powder [J]. Modelling and Simulation in Materials Science and Engineering, 1994, 2: 535–550. doi: 10.1088/0965-0393/2/3A/008 [13] HORIE Y, YANO K. Nonequilibrium fluctutations in shock compression of polycrystalline α-Iron [C]//AIP Conference Proceedings, 2002:553–556. [14] 潘昊, 王升涛, 吴子辉, 等. 孪晶对Be材料冲击加-卸载动力学影响的数值模拟研究 [J]. 物理学报, 2018, 67(16): 164601. doi: 10.7498/aps.67.20180451PAN H, WANG S T, WU Z H, et al. Effect of twining on dynamic behaviors of beryllium materials under impact loading and unloading [J]. Acta Physica Sinica, 2018, 67(16): 164601. doi: 10.7498/aps.67.20180451 [15] HAN P, AN X, ZHANG Y, et al. Particulate scale MPFEM modeling on compaction of Fe and Al composite powders [J]. Powder Technology, 2016, 314: 69–77. [16] HUANG F, AN X, ZHANG Y, et al. Multi-particle FEM simulation of 2D compaction on binary Al/SiC composite powders [J]. Powder Technology, 2017, 314: 39–48. doi: 10.1016/j.powtec.2017.03.017 [17] ZHANG J. A study of compaction of composite particles by multi-particle finite element method [J]. Composites Science & Technology, 2009, 69(13): 2048–2053. [18] HERRMANN W. Constitutive equation for the dynamic compaction of ductile porous materials [J]. Journal of Applied Physics, 1969, 40(6): 2490–2499. doi: 10.1063/1.1658021 [19] CARROLL M M, KIM K T, NESTERENKO V F. The effect of temperature on viscoplastic pore collapse [J]. Journal of Applied Physics, 1986, 59(6): 1962–1967. doi: 10.1063/1.336426 [20] JOHNSON J N. Dynamic fracture and spallation in ductile solids [J]. Journal of Applied Physics, 1981, 52(4): 2812–2825. doi: 10.1063/1.329011 [21] MOLINARI A, MERCIER S. Micromechanical modelling of porous materials under dynamic loading [J]. Journal of the Mechanics & Physics of Solids, 2001, 49(7): 1497–1516. [22] ZAVALIANGOS A. A multiparticle simulation of powder compaction using finite element discretization of individual particles [J]. MRS Online Proceedings Library Archive, 2002: 731. [23] ZHANG Y X, AN X Z, ZHANG Y L. Multi-particle FEM modeling on microscopic behavior of 2D particle compaction [J]. Applied Physics A, 2015, 118(3): 1015–1021. doi: 10.1007/s00339-014-8861-x [24] XIN X J, JAYARAMAN P, JIANG G, et al. Explicit finite element method simulation of consolidation of monolithic and composite powders [J]. Metallurgical & Materials Transactions A, 2002, 33(8): 2649–2658. [25] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. doi: 10.1016/0013-7944(85)90052-9 [26] ABAQUS. Abaqus 6.11 analysis user’s manuals [M]. Rising Sun Mills, USA: Dassault Systmes, 2011. [27] BOADE R R. Principal Hugoniot, second-shock Hugoniot, and release behavior of pressed copper powder [J]. Journal of Applied Physics, 1970, 41(11): 4542–4551. doi: 10.1063/1.1658494 [28] BENSON D J. The calculation of the shock velocity-particle velocity relationship for a copper powder by direct numerical simulation [J]. Wave Motion, 1995, 21(1): 85–99. doi: 10.1016/0165-2125(94)00044-6 [29] BORG J P, VOGLER T J. Aspects of simulating the dynamic compaction of a granular ceramic [J]. Modelling & Simulation in Materials Science & Engineering, 2009, 17(4): 045003. [30] WANG L L. Foundations of stress waves [M]. Amsterdam: Elsevier Science Ltd., 2007. -






 下载:
下载: