管廊内燃气爆炸作用下不同抗爆结构性能研究

刘希亮; 李烨; 王新宇; GURKALOFilip

doi:10.11858/gywlxb.20180640

管廊内燃气爆炸作用下不同抗爆结构性能研究

doi: 10.11858/gywlxb.20180640

刘希亮^{1, 2, 3,},
李烨^1,*, ,,
王新宇^{1, 2, 3},
GURKALOFilip¹

1.
河南理工大学土木工程学院，河南焦作　454000
2.
河南省地下工程与灾变防控重点实验室，河南焦作　454000
3.
河南省地下空间开发及诱发灾变防治国际联合实验室，河南焦作　454000

基金项目: 国家自然科学基金（51474097）；河南理工大学青年骨干教师资助计划（2017XQG-08）

详细信息

作者简介:
刘希亮（1964—），男，博士，教授，主要从事岩土工程研究. E-mail：xlliu@hpu.edu.cn

通讯作者:
李　烨（1994—），女，硕士研究生，主要从事岩土工程研究. E-mail：smartliye@sina.com

中图分类号: TU990.3
计量
- 文章访问数: 6695
- HTML全文浏览量: 2696
- PDF下载量: 20
出版历程
- 收稿日期: 2018-09-19
- 修回日期: 2019-01-07

Anti-Explosion Performance of Different Anti-Explosion Structures under Gas Explosion in Pipe Gallery

LIU Xiliang^{1, 2, 3
,},
LI Ye^{1,*
, ,},
WANG Xinyu^{1, 2, 3},
GURKALO Filip¹

1.
School of Civil Engineering, Henan Polytechnic University, Jiaozuo 454000, China
2.
Henan Key Laboratory of Underground Engineering and Disaster Prevention, Jiaozuo 454000, China
3.
International Joint Research Laboratory of Henan Province for Underground Space Development and Disaster Prevention, Jiaozuo 454000, China

摘要

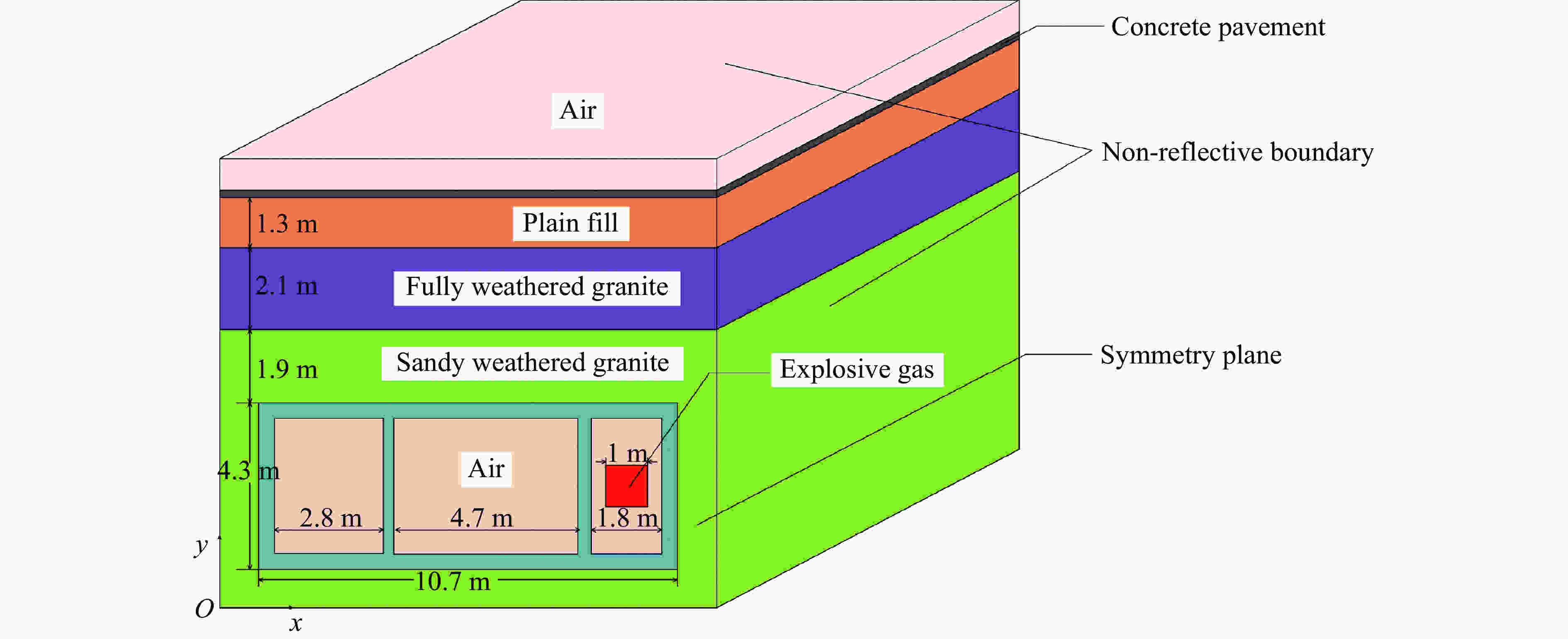
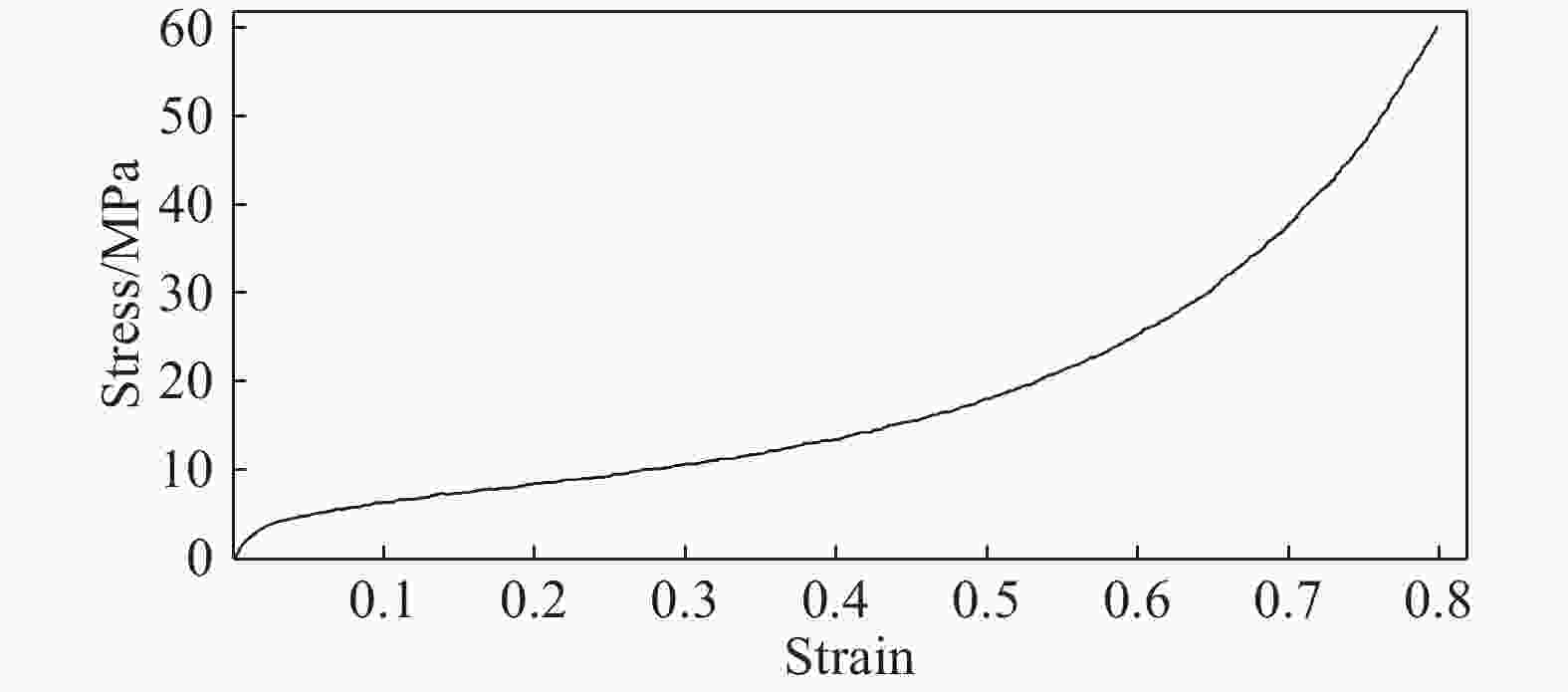
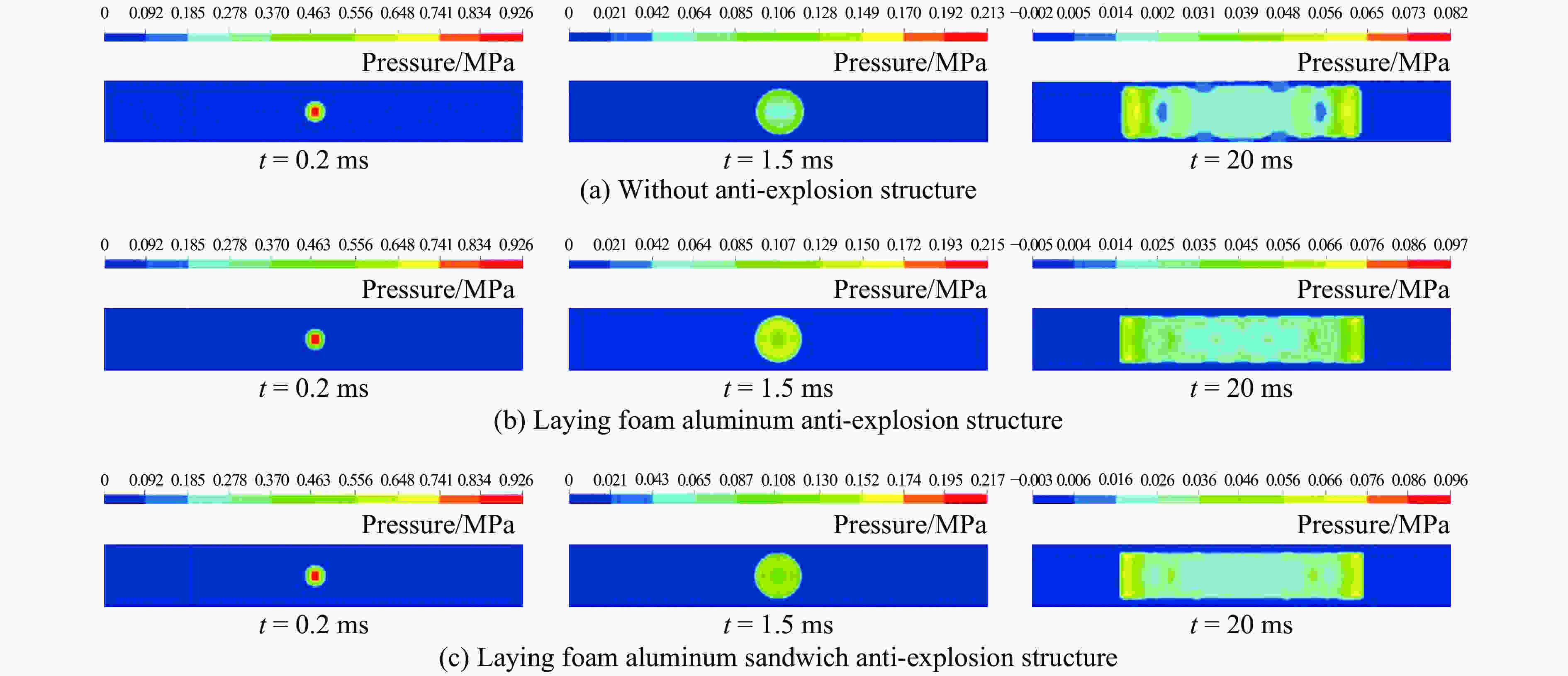
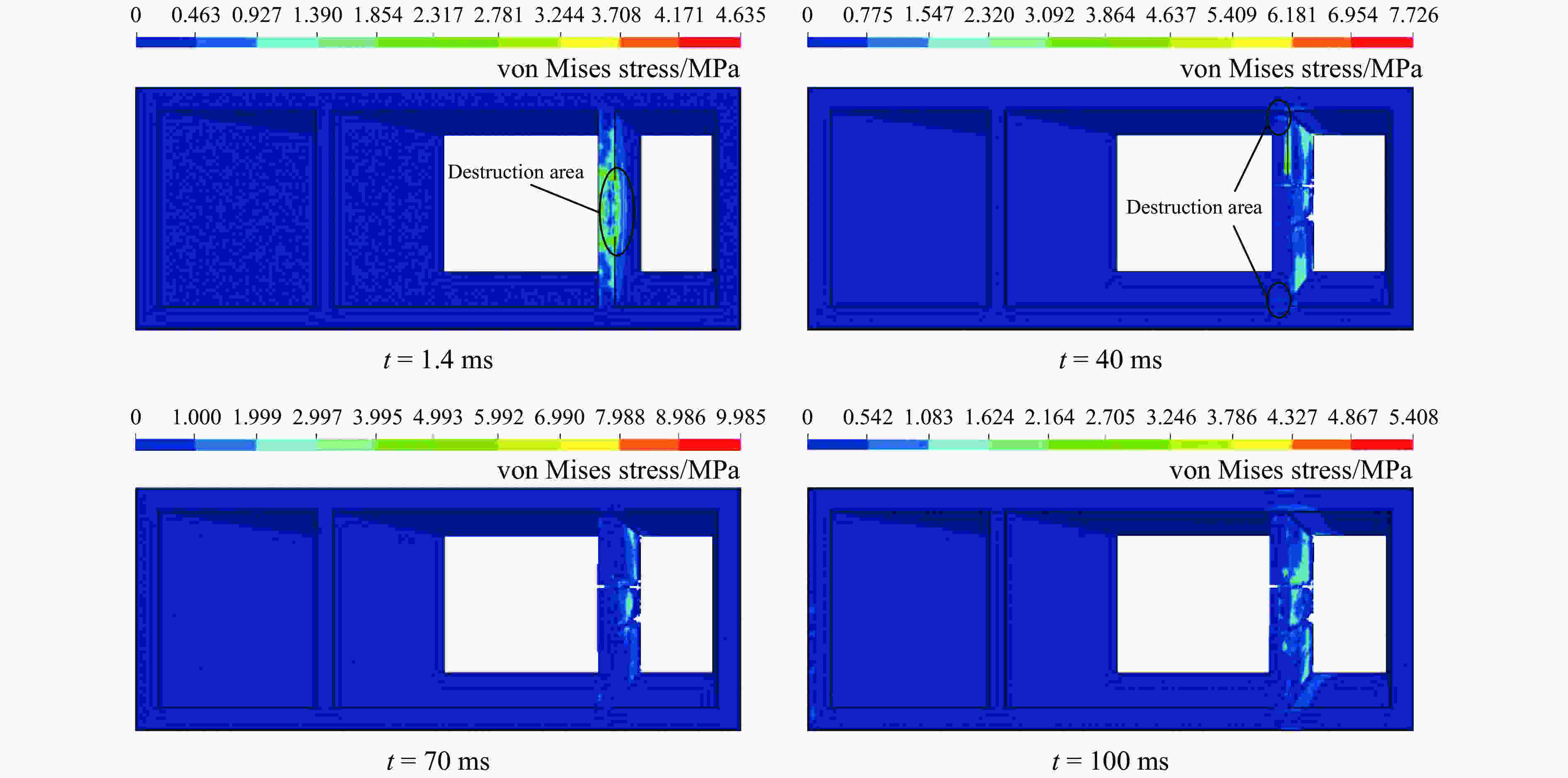
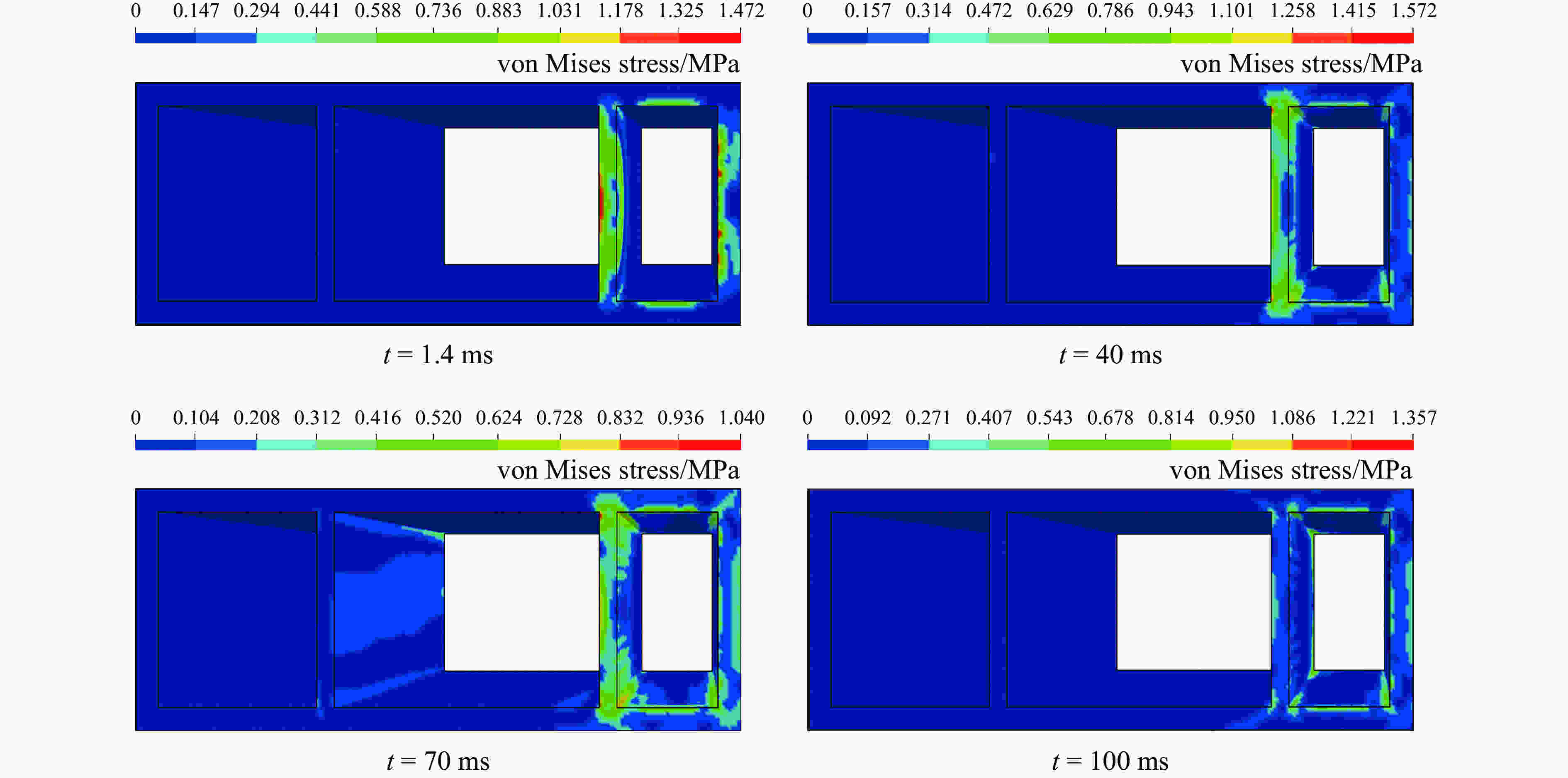
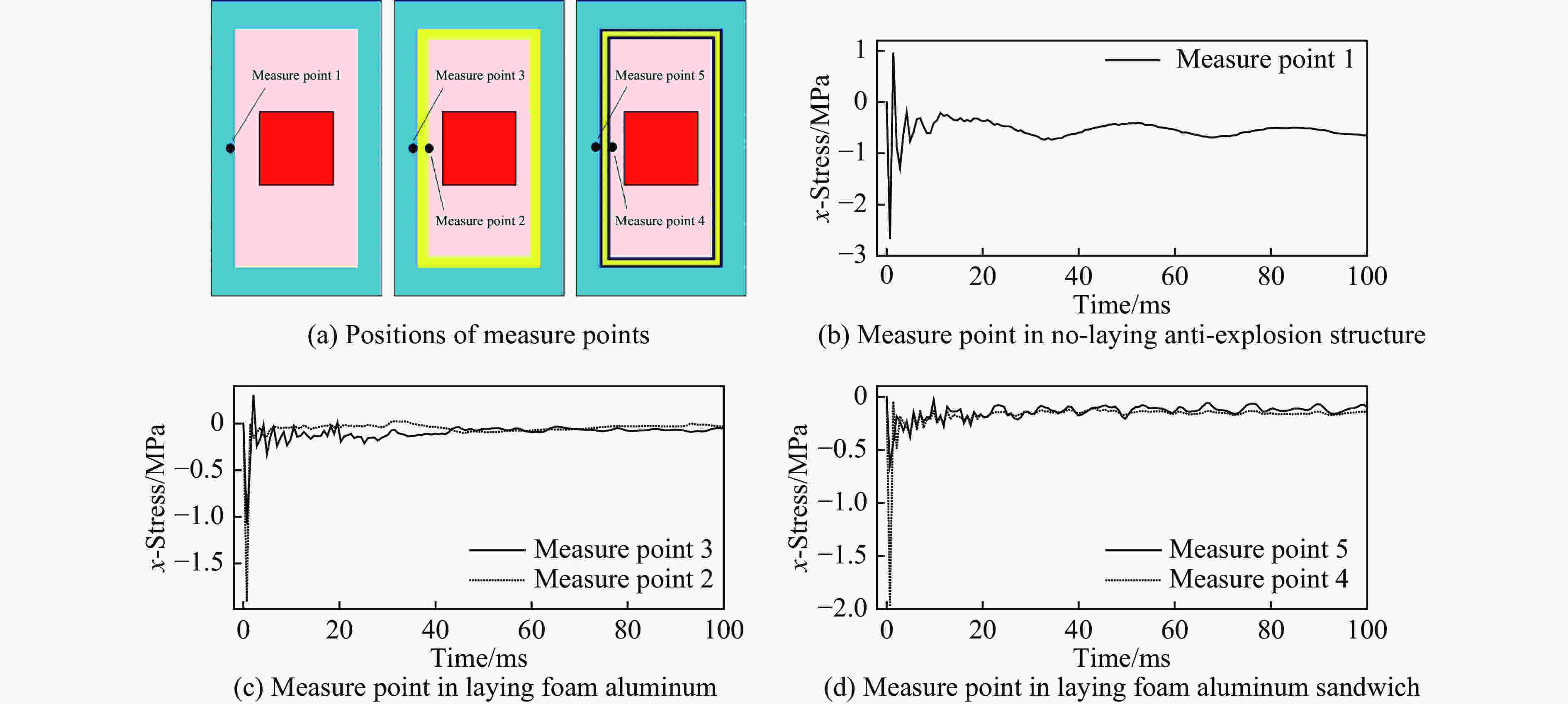
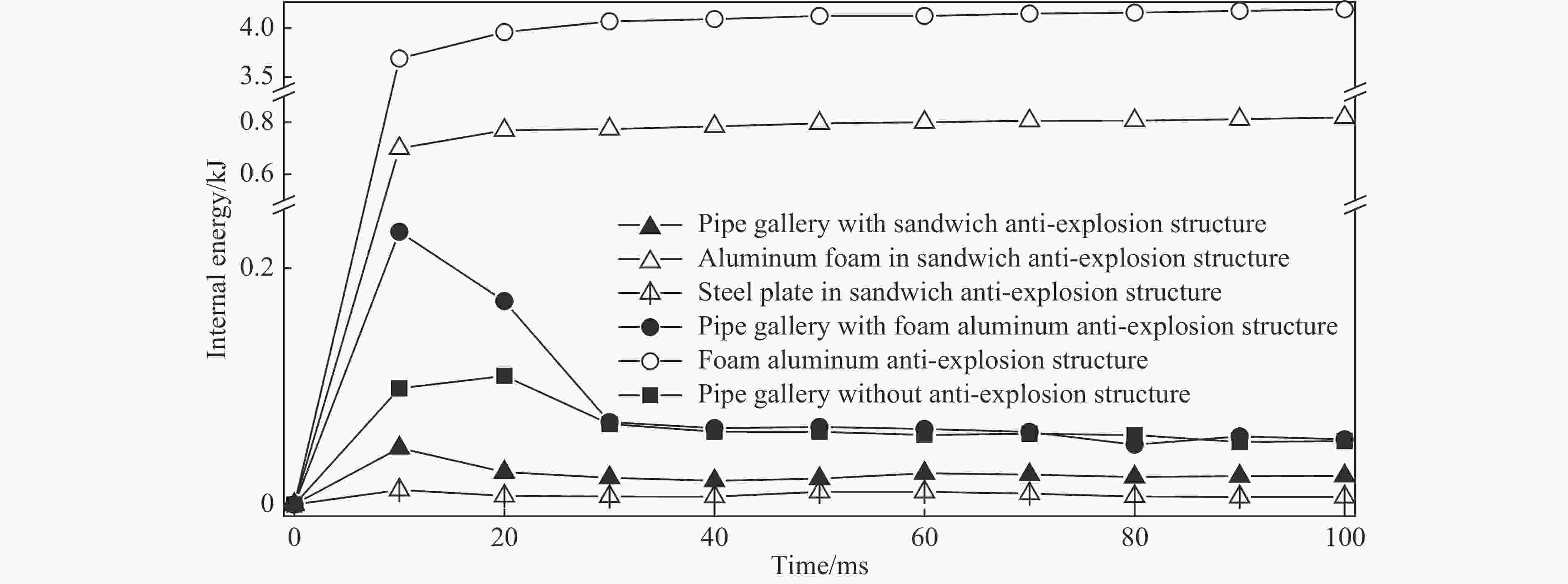
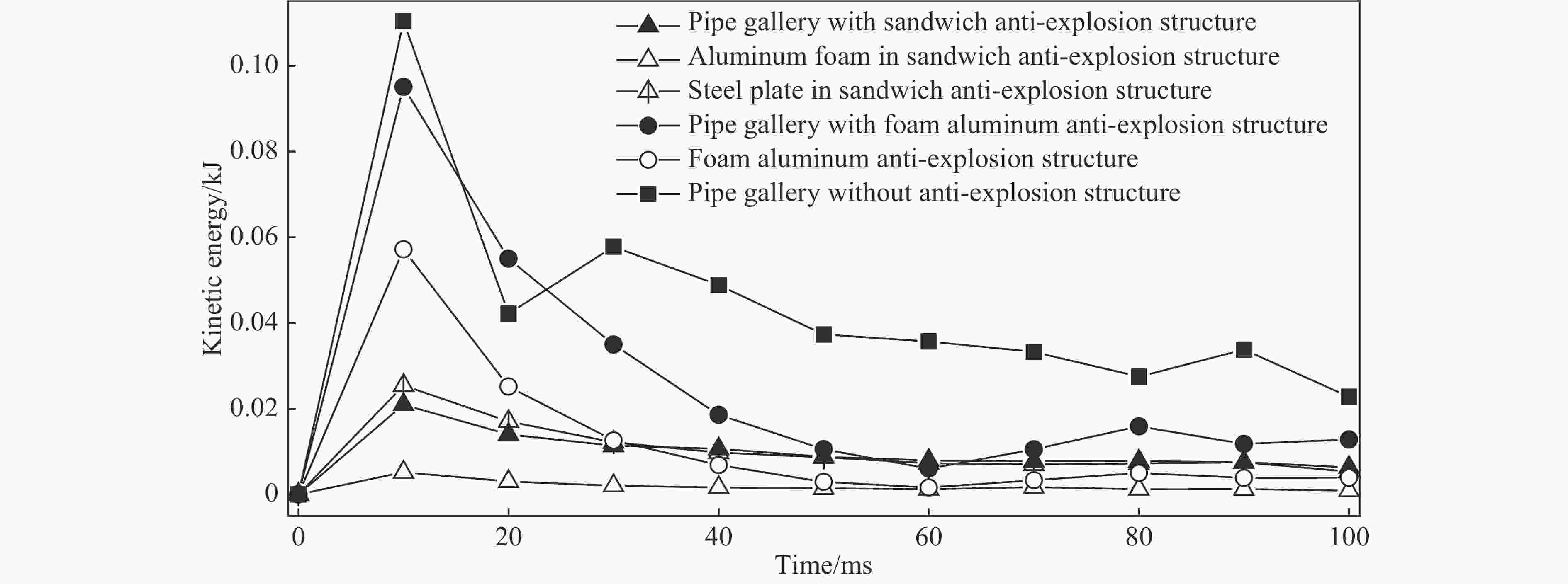
摘要: 地下管廊是城市地下空间的重要组成部分，若燃气在地下管廊输送过程中泄漏进入管廊内部并引起爆炸，将会产生严重的后果。以平潭综合试验区环岛路管线工程为背景，基于流固耦合和ALE(Arbitarty Lagrange Euler)多物质算法，采用ANSYS/LS-DYNA软件建立管廊结构和土体的三维模型，研究地下管廊内燃气爆炸作用下敷设“泡沫铝”抗爆结构和“钢板-泡沫铝-钢板”夹芯抗爆结构的抗爆性能以及管廊的动力响应，并分析不同抗爆结构对管廊结构的应力和变形影响以及抗爆结构的吸能能力。结果表明：爆炸荷载作用下，燃气仓内墙上距离爆炸荷载最近的结构首先发生破坏，随着爆炸进程的发展，燃气仓内墙与外墙连接处也发生破坏；敷设泡沫铝和泡沫铝夹芯结构可以降低廊体结构的损伤，其中又以泡沫铝夹芯结构效果最佳；在泡沫铝夹芯抗爆结构中，结构应力衰减最快，测点应力峰值与无任何抗爆结构的管廊相比降低了67.35%，而在泡沫铝抗爆结构中应力峰值仅降低了43.99%；关于抗爆结构吸能方面，在无任何抗爆结构的管廊内，管廊动能峰值为0.11 kJ，而复合抗爆结构管廊的动能峰值仅为0.021 kJ，与无任何抗爆结构的管廊相比，动能降低了80.9%。综合研究发现，管廊内敷设泡沫铝夹芯结构时吸能和抵抗爆炸冲击波能力最佳。
- 地下工程 /
- 抗爆性 /
- 数值模拟 /
- 综合管廊 /
- 吸能材料
Abstract: The project of loop pipeline in Pingtan test area is used as the engineering background. To compare the anti-explosion performance of " foam aluminum” and " steel plate-foamed aluminum-steel plate” anti-explosion structure under gas explosion, a 3D pipe gallery and soil structure is studied and analyzed by ANSYS/LS-DYNA. The results show that: the structure closest to the explosion gas on the internal wall is broken down at first followed by the damaging of the joint structure of interior and exterior wall in the gas cabin. The stress in the aluminum foam sandwich structure attenuates most quickly. Measuring point peak stress can be reduced as much as 67.35% by aluminum foam sandwich structure compared with no explosion-proof structure. Measuring point peak stress is reduced by 43.99% by aluminum foam structure. The kinetic energy peak value of gallery without anti-explosion is 0.11 kJ. The kinetic energy peak value of gallery with aluminum foam sandwich is 0.021 kJ. By comparison to the gallery without any explosion-proof structure, the kinetic energy is reduced by 80.9%. A comprehensive suggestion is that, laying aluminum foam and aluminum foam core material can reduce the damage of the corridor structure, and the aluminum foam sandwich structure behaves the best.
- underground engineering /
- anti-explosion performance /
- numerical simulation /
- pipe gallery /
- energy absorbing material

HTML全文

图 1 管廊截面图（单位：m）

Figure 1. Underground pipe gallery section（Unit：m）

下载: 全尺寸图片幻灯片

图 2 计算模型爆炸中心截面图

Figure 2. Cross section of the explosion center of the model

下载: 全尺寸图片幻灯片

图 3 添加抗爆结构

Figure 3. With anti-explosion structure

下载: 全尺寸图片幻灯片

图 4 泡沫铝的应力-应变曲线

Figure 4. Stress-strain curve of aluminum foams

下载: 全尺寸图片幻灯片

图 5 冲击波超压云图

Figure 5. Overpressure image of shock wave

下载: 全尺寸图片幻灯片

图 6 无抗爆结构管廊von-Mises应力云图

Figure 6. von-Mises stress map of no explosion-proof pipe gallery

下载: 全尺寸图片幻灯片

图 7 泡沫铝抗爆结构管廊von-Mises应力云图

Figure 7. von-Mises stress map of foamed aluminium explosion-proof pipe gallery

下载: 全尺寸图片幻灯片

图 8 复合抗爆结构管廊von-Mises应力云图

Figure 8. von-Mises stress map of composite explosion-proof pipe gallery

下载: 全尺寸图片幻灯片

图 9 测点x方向应力时程曲线

Figure 9. x-stress of the test point versus time

下载: 全尺寸图片幻灯片

图 10 内能时程曲线图

Figure 10. Internal energy versus time

下载: 全尺寸图片幻灯片

图 11 动能时程曲线图

Figure 11. Kinetic energy versus time

下载: 全尺寸图片幻灯片

表 1 土壤材料参数

Table 1. Parameters of soil material

Material	Thickness/ cm	Density/ （g·cm^–3）	Cohesion/ kPa	Internal friction angle/（°）	Elastic modulus/GPa	Poisson’s ratio
Plain fill	130	1.8	6	10	0.0042	0.30
Completely decomposed granite	210	1.9	20	25	0.02	0.24
Sandy strongly weathered granite	620	2.0	30	32	54	0.21

下载: 导出CSV

表 2 线性多项式状态方程参数^[21]

Table 2. Parameters for linear polynomial equation of state^[21]

Material	$\rho $/（kg·m^–3）	C₀/MPa	C₁	C₂	C₃	C₄	C₅	C₆	E₀/（MJ·m^–3）	V₀
Air	1.234	–0.1	0	0	0	0.400	0.400	0	0.250	1.0
CH₄-Air	1.293	0	0	0	0	0.274	0.274	0	3.408	1.0

下载: 导出CSV

表 3 混凝土和钢材料参数

Table 3. Parameters of concrete and steel

Material	Density/ （g·cm^–3）	Elastic modulus/GPa	Poisson’s ratio	Yield strength/MPa	Shear modulus/GPa	Tensile strength/MPa
Reinforced concrete	2.5	30	0.22	33.8	12.5	3.5
Steel	7.9	220	0.30	314	20	600

下载: 导出CSV

参考文献(21)

[1]	雷升祥. 综合管廊与管道盾构 [M]. 北京: 中国铁道出版社, 2016. LEI S X. Utility tunnel and pipeline shield [M]. Beijing: China Railyway Press, 2016.
[2]	钱七虎, 陈晓强. 国内外地下综合管线廊道发展的现状、问题及对策 [J]. 地下空间与工程学报, 2007, 3(2): 191–194. QIAN Q H, CHEN X Q. Situation problems and countermeasures of utility tunnel development in China and abroad [J]. Chinese Journal of Underground Space and Engineering, 2007, 3(2): 191–194.
[3]	WILLIAMSON E B, BAYRAK O, DAVIS C, et al. Performance of bridge columns subjected to blast loads Ⅰ: experimental program [J]. Journal of Bridge Engineering, 2011, 16(6): 693–702. doi: 10.1061/(ASCE)BE.1943-5592.0000220
[4]	OLMATI P, PETRINI F, GKOUMAS K. Fragility analysis for the performance-based design of cladding wall panels subjected to blast load [J]. Engineering Structures, 2014, 78: 112–120. doi: 10.1016/j.engstruct.2014.06.004
[5]	丁阳, 方磊, 李忠献, 等. 防恐建筑结构抗爆防护分类设防标准研究 [J]. 建筑结构学报, 2013, 34(4): 57–64. DING Y, FANG L, LI Z X, et al. Research on categorized explosion protection criterion of anti-terrorism building structures [J]. Journal of Building Structures, 2013, 34(4): 57–64.
[6]	闫秋实, 刘晶波, 伍俊. 典型地铁车站内爆炸致人员伤亡区域的预测研究 [J]. 工程力学, 2012, 29(2): 81–88. YAN Q S, LIU J B, WU J. Estimation of casually areas in subway station subjected to terrorist bomb [J]. Engineering Mechanics, 2012, 29(2): 81–88.
[7]	于润清, 方秦, 陈力, 等. 建筑结构构件基于性能的抗爆设计方法 [J]. 工程力学, 2016, 33(11): 75–83. doi: 10.6052/j.issn.1000-4750.2015.04.0280 YU R Q, FANG Q, CHEN L, et al. Performance-based blast-resistant design of building structure components [J]. Engineering Mechanics, 2016, 33(11): 75–83. doi: 10.6052/j.issn.1000-4750.2015.04.0280
[8]	宋彬, 黄正祥, 翟文, 等. 聚脲弹性体夹芯防爆罐抗爆性能研究 [J]. 振动与冲击, 2016, 35(7): 138–144. SONG B, HAUNG Z X, ZHAI W, et al. Anti-detonation properties of explosion-proof pots made of sandwich structure with polyurea elastomer [J]. Journal of Vibration and Shock, 2016, 35(7): 138–144.
[9]	任新见, 李广新, 张胜民. 泡沫铝夹心排爆罐抗爆性能试验研究 [J]. 振动与冲击, 2011, 30(5): 213–217. doi: 10.3969/j.issn.1000-3835.2011.05.044 REN X J, LI G X, ZHANG S M. Antidetonation property tests for explosion-proof pots made of sandwich structure with aluminum foam [J]. Journal of Vibration and Shock, 2011, 30(5): 213–217. doi: 10.3969/j.issn.1000-3835.2011.05.044
[10]	TEKALUR S A, SHUKLA A, SHIVAKUMAR K. Blast resistance of polyurea based layered composite materials [J]. Composite Structures, 2008, 84(3): 271–281. doi: 10.1016/j.compstruct.2007.08.008
[11]	张秀华. 气体爆炸冲击作用下钢框架康保性能试验研究与数值模拟 [D]. 哈尔滨: 哈尔滨工业大学, 2011. ZHANG X H. Experimental research and numerical simulation on blast resistance performance of steel frames [D]. Harbin: Harbin Institute of Technology, 2011.
[12]	李忠献, 刘杨, 田力. 单侧隧道内爆炸荷载作用下双线地铁隧道的动力响应与抗爆分析 [J]. 北京工业大学学报, 2006, 32(2): 173–181. doi: 10.3969/j.issn.0254-0037.2006.02.014 LI Z X, LIU Y, TIAN L. Dynamic response and blast-resistance analysis of double track subway tunnel subkected to blast loading within one side of tunnel [J]. Journal of Beijing University of Technology, 2006, 32(2): 173–181. doi: 10.3969/j.issn.0254-0037.2006.02.014
[13]	刘颖芳, 刘仁辉, 石少卿, 等. 应用泡沫铝降低地下爆炸冲击波的数值分析 [J]. 地下空间与工程学报, 2008, 4(2): 230–233. LIU Y F, LIU R H, SHI S Q, et al. Numerical simulation analysis of reducing blast by using foam aluminum [J]. Chinese Journal of Underground Space and Engineering, 2008, 4(2): 230–233.
[14]	GOEL M D, MATSAGAR V A, GUPTA A K. Blast resistance of stiffened sandwich panels with closed-cell aluminum foam [J]. Latin American Journal of Solids and Structures, 2014, 11(13): 2497–2515. doi: 10.1590/S1679-78252014001300010
[15]	夏志成, 王曦浩, 赵跃堂, 等. 钢板夹泡沫铝组合板抗接性能研究 [J]. 振动与冲击, 2017, 36(2): 117–122. XIA Z C, WANG X H, ZHAO Y T, et al. Anti-blast performance of aluminum foam-core sandwich panels [J]. Journal of Vibration and Shock, 2017, 36(2): 117–122.
[16]	DHARMASENA K P, WADLEY H N G, XUE Z Y, et al. Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamic loading [J]. International Journal of Impact Engineering, 2008, 35(9): 1063–1074. doi: 10.1016/j.ijimpeng.2007.06.008
[17]	张旭红, 王志华, 赵隆茂. 爆炸荷载下铝蜂窝夹芯板动力响应研究 [J]. 应用力学学报, 2009, 26(2): 2459–2463. ZHANG X H, WANG Z H, ZHAO L M. Dynamic plastic response of sandwich plate with aluminum honeycombs core under blast loading [J]. Chinese Journal of Applied Mechanics, 2009, 26(2): 2459–2463.
[18]	杨德庆, 马涛, 张梗林. 舰艇新型宏观负泊松比效应蜂窝舷侧防护结构 [J]. 爆炸与冲击, 2015, 35(2): 243–248. doi: 10.11883/1001-1455(2015)02-0243-06 YANG D Q, MA T, ZHANG G L. A novel auxetic broadside defensive structure for naval ships [J]. Explosion and Shock Waves, 2015, 35(2): 243–248. doi: 10.11883/1001-1455(2015)02-0243-06
[19]	Livermore Software Technology Corporation. LS-DYNA keyword user’s manual [Z]. Livermore, CA: Livermore Software Technology Corporation, 2006.
[20]	赵衡阳. 气体和粉尘爆炸原理 [M]. 北京: 北京理工大学出版社, 1996. ZHAO H Y. The principle of gas and dust explosion [M]. Beijing: Beijing Institute of Technology Press, 1996.
[21]	吴燕燕. 室内燃气爆炸作用下钢框架结构动力响应与连续倒塌分析 [D]. 哈尔滨: 东北林业大学, 2012. WU Y Y. Analysis on dynamic responses and progressive collapse of steel frame structure subject ti internal gas explosion [D]. Harbin: Northeast Forestry University, 2012.