-
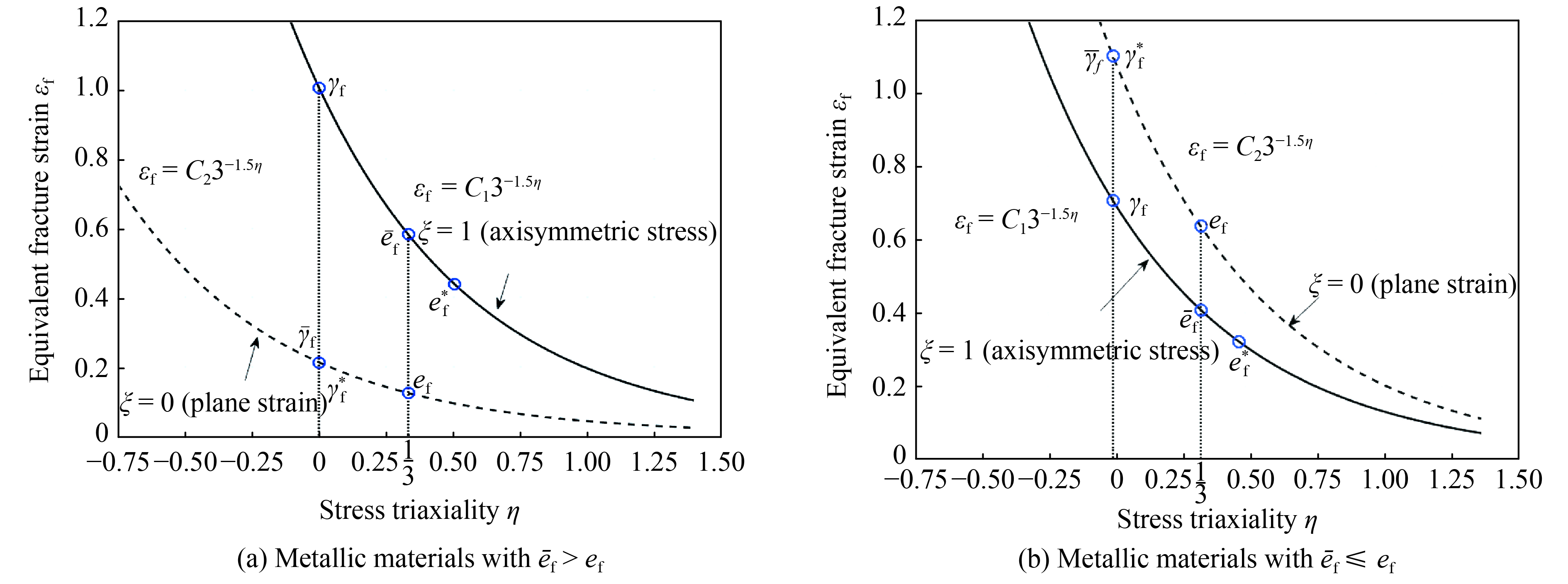
摘要: 提出了一种预测金属材料失效的新方法,该失效准则考虑了应力三轴度和Lode角参数的影响。将金属材料分为 ēf>ef 和 ēf≤ef 两类,其中 ēf 和 ef 分别定义为应力三轴度η=1/3、Lode角参数ξ=1(轴对称应力状态)和应力三轴度η=1/3、Lode角参数ξ=0(平面应变状态)时的真实应变。另外只需要两个常见的实验(光滑圆杆拉伸试验和纯剪试验)数据就可以确定失效准则的参数值。将该新失效准则与文献中报道的诸多材料在不同加载条件下的实验数据进行对比,结果吻合较好。Abstract: A new approach is presented herein to predict the failure of metallic materials. A failure criterion that caters for the effects of stress triaxiality and Lode parameter is proposed and it is applicable not only to metals with ēf > ef but also to metals with ēf ≤ ef , here ēf and ef are the two parameters defined as the true strains at stress triaxiality of η = 1/3 for Lode parameters of ξ = 1 (axisymmetric stress state) and ξ = 0 (plane strain state) respectively. Furthermore, only two laboratory tests such as smooth bar tension test and pure shear test are needed to calibrate the failure criterion. The present failure criterion is proved in good agreement with the test data for various metals under different loading conditions.
-
Key words:
- failure criterion /
- metallic material /
- stress triaxiality /
- Lode parameter /
- smooth bar tension test /
- pure shear test
-
Figure 8. Comparison of the newly developed failure criterion with the test data for 2024-T351 aluminum alloy (Wierzbicki et al.[6]; Bao[14]) in the space of εf and η. Red line: Johnson-Cook failure criterion[2]; green lines: the model proposed by Xue and Wierzbicki[6]; black lines: the present model (Eq.(8))
Table 1. Values of constants in the Johnson-Cook failure criterion[2] and the model proposed by Xue and Wierzbicki[6]
Materials Johnson-Cook failure criterion Model proposed by Xue and Wierzbicki D1 D2 D3 c1 c2 c3 c4 4340 steel 0.05[2] 3.44[2] –2.12[2] Armco iron –2.20[2] 5.43[2] –0.47[2] OFHC copper 0.54[2] 4.89[2] –3.03[2] 1045 steel 0.06 1.72 –2.58 1.511 0 2.110 2 0.480 0 1.738 8 2024-T351 0.13[6] 0.13[6] –1.50[6] 1.466 0 2.394 0 0.210 0 0.005 0 Inconel 718[16] 0.04[16] 0.75[16] –1.45[16] 0.525 1 1.010 9 1.100 0 1.188 7 Inconel 718[18] 0.04 1.54 –1.60 -
[1] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//Proceedings of the 7th International Symposium on Ballistics, 1983, 21: 541-547. [2] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48. doi: 10.1016/0013-7944(85)90052-9 [3] ALVES M, JONES N. Influence of hydrostatic stress on failure of axisymmetric notched specimens [J]. Journal of the Mechanics & Physics of Solids, 1999, 47(3): 643–667. [4] BØRVIK T, HOPPERSTAD O S, BERSTAD T. On the influence of stress triaxiality and strain rate on the behaviour of a structural steel. Part II. numerical study [J]. European Journal of Mechanics A/Solids, 2003, 22(1): 15–32. doi: 10.1016/S0997-7538(02)00005-0 [5] BAO Y, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space [J]. International Journal of Mechanical Sciences, 2004, 46(1): 81–98. doi: 10.1016/j.ijmecsci.2004.02.006 [6] WIERZBICKI T, BAO Y, LEE Y W. Calibration and evaluation of seven fracture models [J]. International Journal of Mechanical Sciences, 2005, 47(4): 719–743. [7] XUE L. Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading [J]. International Journal of Solids and Structures, 2007, 44(16): 5163–5181. doi: 10.1016/j.ijsolstr.2006.12.026 [8] BAI Y, WIERZBICKI T. A new model of metal plasticity and fracture with pressure and Lode dependence [J]. International Journal of Plasticity, 2008, 24(6): 1071–1096. doi: 10.1016/j.ijplas.2007.09.004 [9] BAI Y, WIERZBICKI T. Application of extended Mohr-Coulomb criterion to ductile fracture [J]. International Journal of Fracture, 2010, 161(1): 1–20. doi: 10.1007/s10704-009-9422-8 [10] CHOCRON S, ERICE B, ANDERSON C E. A new plasticity and failure model for ballistic application [J]. International Journal of Impact Engineering, 2011, 38(8): 755–764. [11] BRÜNIG M, CHYRA O, ALBRECHT D. A ductile damage criterion at various stress triaxialities [J]. International Journal of Plasticity, 2008, 24: 1731–1755. doi: 10.1016/j.ijplas.2007.12.001 [12] MALCHER L, PIRES F M A, SÁ J M A C D. An extended GTN model for ductile fracture under high and low stress triaxiality [J]. International Journal of Plasticity, 2014, 54(2): 193–228. [13] RICE J R, TRACEY D. On the ductile enlargement of voids in triaxial stress fields [J]. Journal of the Mechanics & Physics of Solids, 1969, 17(3): 201–217. [14] BAO Y. Prediction of ductile crack formation in uncracked bodies [D]. Boston, Massachusetts: Massachusetts Institute of Technology, 2003. [15] BAI Y, TENG X, WIERZBICKI T. On the application of stress triaxiality formula for plane strain fracture testing [J]. Journal of Engineering Materials and Technology, 2009, 131(2): 021002. doi: 10.1115/1.3078390 [16] ERICE B, GÁLVEZ F. A coupled elastoplastic-damage constitutive model with Lode angle dependent failure criterion [J]. International Journal of Solids and Structures, 2014, 51(1): 93–110. doi: 10.1016/j.ijsolstr.2013.09.015 [17] ERICE B, PÉREZ-MARTÍN M, GÁLVEZ F. An experimental and numerical study of ductile failure under quasi-static and impact loadings of Inconel 718 nickel-base superalloy [J]. International Journal of Impact Engineering, 2014, 69: 11–24. doi: 10.1016/j.ijimpeng.2014.02.007 [18] ALGARNI M, BAI Y, YOUNGSIK C. A study of Inconel 718 dependency on stress triaxiality and Lode angle in plastic deformation and ductile fracture [J]. Engineering Fracture Mechanics, 2015, 147: 140–157. doi: 10.1016/j.engfracmech.2015.08.007 -






 下载:
下载: