Preliminary Investigation on Stress Distribution Mechanism of Shock Propagating across Grain Interface in Metal
-
摘要: 冲击波跨越晶界过程中的应力分配机制对于深入理解冲击波与多晶金属材料的相互作用现象和塑性机理有重要意义。为探明该机制,采用分子动力学,对4种面心立方(FCC)晶格金属展开研究,细致统计分析了冲击波在单晶金属{100}晶面内随晶向角变化的应力生成特征及冲击波跨过单一晶界前后的应力状态和大小关系。结果表明:(1)垂直和平行于冲击波运动方向的应力分量随晶向角呈现不同的变化特征,这种应力生成差异的根源来自晶格原子排列导致的受力差异和原子间作用力机制,而其生成差异的结果恰恰是不同晶向塑性差异的主要原因;(2)弹性冲击波跨过单一晶界前后的应力状态存在一定的分配转换关系,由一个独立的应力分配张量D确定,不同FCC晶格元素的D张量形式一致,系数差异小,具有一定的通用特征;(3)验证表明,对于给定的FCC晶格金属,D具有一致的可预测特性,反映了冲击波与晶格相互作用的本质特征。Abstract: To know the stress distribution mechanism of shock propagating across grain interface is of great significance to understand the interacting phenomena and plastic principles of shock and polycrystalline metal material. With molecular dynamics (MD), shock impacting on four kinds of metals with FCC (face-centered cubic) crystal lattice are numerically simulated. The stress tensor components distribution, scale and correlations of shock propagating in monocrystal and across grain interface on {100} lattice plane are computed and analyzed. It is concluded as follows: (1) The stress generated after shock propagating along different lattice arrangement orientations presents different characteristics between parallel and perpendicular shock direction, which is in accordance with force interaction difference due to the lattice arrangement and interaction mechanism between atoms. The results of such difference are corresponding to the plasticity variation with lattice orientations. (2) An independent tensor is found to be in charge of stress distribution in elastic shock propagating across a single grain interface. This tensor has uniform style and similar coefficients for different materials with the same lattice arrangement, presenting a kind of generality. (3) The coherent predictability and accuracy of stress distribution tensor for FCC lattice are validated by simulation results for shock impacting on a single grain interfaces at different velocities and lattice arrangement orientations, indicating the intrinsic property of the interaction between shock and lattice atoms.
-
Key words:
- polycrystalline metal /
- shock wave /
- grain interface /
- face-centered cubic /
- stress /
- molecular dynamics
-
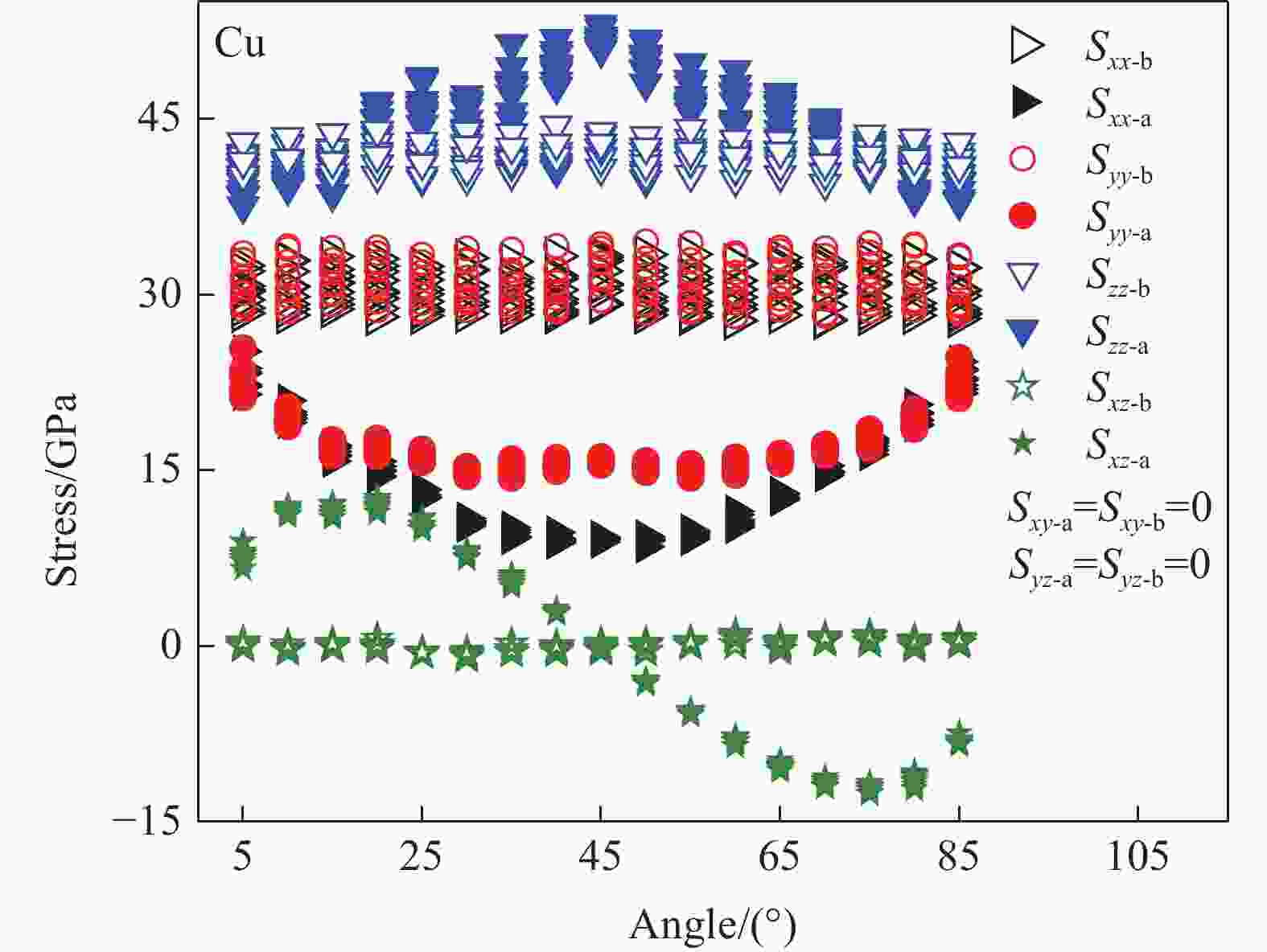
图 4 vp= 1 km/s冲击下t=10 ps时不同晶向单晶铜的原子排列(色彩表示不同的晶格形式)以及应力张量分量(Sxx, Syy, Szz)分布差异(从左往右晶格角度
$\theta $ 从0°到90°,$\Delta \theta $ = 15°)Figure 4. Snapshot of lattice arrangement and stress tensor components (Sxx, Syy, Szz) of monocrystal copper at t = 10 ps under impact of vp = 1 km/s(Lattice arrangement orientation
$\theta $ = 0° –90°,$\Delta \theta $ = 15°) -
[1] CAO B, BRINGA E M, MEYERS M A. Shock compression of monocrystalline copper: atomistic simulations [J]. Metallurgical and Materials Transactions A, 2007, 38(11): 2681–2688. doi: 10.1007/s11661-007-9248-9 [2] BRINGA E M, CAZAMIAS J U, ERHART P, et al. Atomistic shock Hugoniot simulation of single-crystal copper [J]. Journal of Applied Physics, 2004, 96(7): 3793–3799. doi: 10.1063/1.1789266 [3] BRINGA E M, ROSOLANKOVA K, RUDD R E, et al. Shock deformation of face-centred-cubic metals on subnanosecond timescales [J]. Nature Materials, 2006, 5(10): 805–809. doi: 10.1038/nmat1735 [4] BRINGA E M, CARO A, VICTORIA M, et al. The atomistic modeling of wave propagation in nanocrystals [J]. JOM, 2005, 57(9): 67–70. doi: 10.1007/s11837-005-0119-9 [5] BRINGA E M, CARO A, WANG Y, et al. Ultrahigh strength in nanocrystalline materials under shock loading [J]. Science, 2005, 309(5742): 1838–1841. doi: 10.1126/science.1116723 [6] WANG Y M, BRINGA E M, MCNANEY J M, et al. Deforming nanocrystalline nickel at ultrahigh strain rates [J]. Applied Physics Letters, 2006, 88(6): 061917. doi: 10.1063/1.2173257 [7] NEOGI A, MITRA N. A metastable phase of shocked bulk single crystal copper: an atomistic simulation study [J]. Scientific Reports, 2017, 7(1): 7337. doi: 10.1038/s41598-017-07809-1 [8] KADAU K, GERMANN T C, LOMDAHL P S, et al. Shock waves in polycrystalline iron [J]. Physical Review Letters, 2007, 98(13): 135701. doi: 10.1103/PhysRevLett.98.135701 [9] 赵丰鹏. 纳米多孔金属铜冲击响应的分子动力学模拟研究 [D]. 合肥: 中国科学技术大学, 2014.ZHAO F P. Molecular dynamic simulationj on shock response of nanoporous Cu [D]. Hefei: University of Science and Technology of China, 2014. [10] 马文, 祝文军, 张亚林, 等. 纳米多晶铁的冲击相变研究 [J]. 物理学报, 2011, 60(6): 066404. doi: 10.7498/aps.60.066404MA W, ZHU W J, ZHANG Y L, et al. Shock-induced phase transformation in nanocrystalline iron [J]. Acta Physica Sinica, 2011, 60(6): 066404. doi: 10.7498/aps.60.066404 [11] 马文, 祝文军, 陈开果, 等. 晶界对纳米多晶铝中冲击波阵面结构影响的分子动力学研究 [J]. 物理学报, 2011, 60(1): 016107. doi: 10.7498/aps.60.016107MA W, ZHU W J, CHEN K G, et al. Molecular dynamics investigation of shock front in nanocrystalline aluminum: grain boundary effects [J]. Acta Physica Sinica, 2011, 60(1): 016107. doi: 10.7498/aps.60.016107 [12] 马文. 冲击压缩下纳米多晶金属塑性及相变机制的分子动力学研究[D]. 长沙: 国防科学技术大学, 2011.MA W. Molecular dynamics investigations on the mechanisms of plastic deformation and phase transformation of nanocrystalline metals under shock compression [D]. Changsha: National University of Defense Technology, 2011. [13] 马文, 陆彦文. 纳米多晶铜中冲击波阵面的分子动力学研究 [J]. 物理学报, 2013, 62(3): 036201. doi: 10.7498/aps.62.036201MA W, LU Y W. Molecular dynamics investigation of shock front in nanocrystalline copper [J]. Acta Physica Sinica, 2013, 62(3): 036201. doi: 10.7498/aps.62.036201 [14] MA W, ZHU W J, JING F Q. The shock-front structure of nanocrystalline aluminum [J]. Applied Physics Letters, 2010, 97(12): 121903. doi: 10.1063/1.3490643 [15] MA W, ZHU W, HOU Y. A comparative study on shock compression of nanocrystalline Al and Cu: shock profiles and microscopic views of plasticity [J]. Journal of Applied Physics, 2013, 114(16): 163504. doi: 10.1063/1.4826624 [16] 陈开果, 祝文军, 马文, 等. 冲击波在纳米金属铜中传播的分子动力学模拟 [J]. 物理学报, 2010, 59(2): 1225–1232. doi: 10.7498/aps.59.1225CHEN K G, ZHU W J, MA W, et al. Propagation of shockwave in nanocrystalline copper: molecular dynamics simulation [J]. Acta Physica Sinica, 2010, 59(2): 1225–1232. doi: 10.7498/aps.59.1225 [17] 邵建立, 王裴, 何安民, 等. 冲击诱导金属铝表面微射流现象的微观模拟 [J]. 物理学报, 2012, 61(18): 184701. doi: 10.7498/aps.61.184701SHAO J L, WANG P, HE A M, et al. Microscopic simulation on shock-induced micro-jet ejection from metal Al surface [J]. Acta Physica Sinica, 2012, 61(18): 184701. doi: 10.7498/aps.61.184701 [18] 邵建立, 秦承森, 王裴. 动态压缩下马氏体相变力学性质的微观研究 [J]. 物理学报, 2009, 58(3): 1936–1941. doi: 10.3321/j.issn:1000-3290.2009.03.087SHAO J L, QIN C S, WANG P. Atomistic simulation of mechanical properties of martensitic transformation under dynamic compression [J]. Acta Physica Sinica, 2009, 58(3): 1936–1941. doi: 10.3321/j.issn:1000-3290.2009.03.087 [19] 邵建立, 王裴, 秦承森, 等. 铁冲击相变的分子动力学研究 [J]. 物理学报, 2007, 56(9): 5389–5393. doi: 10.3321/j.issn:1000-3290.2007.09.067SHAO J L, WANG P, QIN C S, et al. Shock-induced phase transformations of iron studied with molecular dynamics [J]. Acta Physica Sinica, 2007, 56(9): 5389–5393. doi: 10.3321/j.issn:1000-3290.2007.09.067 [20] 何安民, 邵建立, 秦承森, 等. 单晶Cu冲击加载及卸载下塑性行为的微观模拟 [J]. 物理学报, 2009, 58(8): 5667–5672. doi: 10.3321/j.issn:1000-3290.2009.08.082HE A M, SHAO J L, QIN C S, et al. Molecular dynamics study on the plastic behavior of monocrystalline copper under shock loading and unloading [J]. Acta Physica Sinica, 2009, 58(8): 5667–5672. doi: 10.3321/j.issn:1000-3290.2009.08.082 [21] ARMAN B, LUO S N, GERMANN T C, et al. Dynamic response of Cu46Zr54 metallic glass to high-strain-rate shock loading: plasticity, spall, and atomic-level structures [J]. Physical Review B, 2010, 81(14): 144201. doi: 10.1103/PhysRevB.81.144201 [22] ZONG H, LOOKMAN T, DING X, et al. Anisotropic shock response of titanium: reorientation and transformation mechanisms [J]. Acta Materialia, 2014, 65(4): 10–18. [23] XIE Y, HAN L B, AN Q, et al. Release melting of shock-loaded single crystal Cu [J]. Journal of Applied Physics, 2009, 105(6): 066103. doi: 10.1063/1.3099597 [24] LUO S N, GERMANN T C, TONKS D L. The effect of vacancies on dynamic response of single crystal Cu to shock waves [J]. Journal of Applied Physics, 2010, 107(5): 056102. doi: 10.1063/1.3326941 [25] YU Y, LI C, MA H H, et al. Deformation and spallation of explosive welded steels under gas gun shock loading [J]. Chinese Physics Letters, 2018, 35(1): 018101. doi: 10.1088/0256-307X/35/1/018101 [26] LUO S N, GERMANN T C, DESAI T G, et al. Anisotropic shock response of columnar nanocrystalline Cu [J]. Journal of Applied Physics, 2010, 107(12): 123507. doi: 10.1063/1.3437654 [27] LUO S N, GERMANN T C, TONKS D L, et al. Shock wave loading and spallation of copper bicrystals with asymmetric Σ3〈110〉tilt grain boundaries [J]. Journal of Applied Physics, 2010, 108(9): 093526. doi: 10.1063/1.3506707 [28] WANG L, ZHAO F, ZHAO F P, et al. Grain boundary orientation effects on deformation of Ta bicrystal nanopillars under high strain-rate compression [J]. Journal of Applied Physics, 2014, 115(5): 053528. doi: 10.1063/1.4864427 [29] CAO F, BEYERLEIN I J, ADDESSIO F L, et al. Orientation dependence of shock-induced twinning and substructures in a copper bicrystal [J]. Acta Materialia, 2010, 58(2): 549–559. doi: 10.1016/j.actamat.2009.09.033 [30] MEYERS M A, CARVALHO M S. Shock-front irregularities in polycrystalline metals [J]. Materials Science and Engineering, 1976, 24(1): 131–135. doi: 10.1016/0025-5416(76)90102-6 [31] BARBER J L, KADAU K. Shock-front broadening in polycrystalline materials [J]. Physical Review B, 2008, 77(14): 144106. doi: 10.1103/PhysRevB.77.144106 [32] ZHAKHOVSKⅡ V V, ZYBIN S V, NISHIHARA K, et al. Shock wave structure in Lennard-Jones crystal via molecular dynamics [J]. Physical Review Letters, 1999, 83(6): 1175–1178. doi: 10.1103/PhysRevLett.83.1175 [33] GERMANN T C, HOLIAN B L, LOMDAHL P S, et al. Orientation dependence in molecular dynamics simulations of shocked single crystals [J]. Physical Review Letters, 2000, 84(23): 5351–5354. doi: 10.1103/PhysRevLett.84.5351 [34] HOLIAN B L, LOMDAHL P S. Plasticity induced by shock waves in nonequilibrium molecular-dynamics simulations [J]. Science, 1998, 280(5372): 2085–2088. doi: 10.1126/science.280.5372.2085 [35] HOLIAN B L. Molecular dynamics comes of age for shockwave research [J]. Shock Waves, 2004, 13(6): 489–495. [36] KADAU K, GERMANN T C, LOMDAHL P S, et al. Microscopic view of structural phase transitions induced by shock waves [J]. Science, 2002, 296(5573): 1681–1684. doi: 10.1126/science.1070375 [37] GERMANN T C, HOLIAN B L, LOMDAHL P S, et al. Dislocation structure behind a shock front in fcc perfect crystals: atomistic simulation results [J]. Metallurgical and Materials Transactions A, 2004, 35(9): 2609–2615. doi: 10.1007/s11661-004-0206-5 [38] ROBERTSON D H, BRENNER D W, WHITE C T. Split shock waves from molecular dynamics [J]. Physical Review Letters, 1991, 67(22): 3132–3135. doi: 10.1103/PhysRevLett.67.3132 [39] KELCHNER C L, PLIMPTON S J, HAMILTON J C. Dislocation nucleation and defect structure during surface indentation [J]. Physical Review B, 1998, 58(17): 11085–11088. doi: 10.1103/PhysRevB.58.11085 [40] LIU C M, XU C, CHENG Y, et al. Orientation-dependent responses of tungsten single crystal under shock compression via molecular dynamics simulations [J]. Computational Materials Science, 2015, 110: 359–367. doi: 10.1016/j.commatsci.2015.08.051 [41] PLIMPTON S. Fast parallel algorithms for short-range molecular-dynamics [J]. Journal of Computational Physics, 1995, 117(1): 1–19. doi: 10.1006/jcph.1995.1039 [42] ZHOU X W, JOHNSON R A, WADLEY H N G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers [J]. Physical Review B, 2004, 69(14): 144113. doi: 10.1103/PhysRevB.69.144113 [43] Sandia National Laboratories. Lammps users manual [Z]. Albuquerque, NM: Sandia National Laboratories, 2016. [44] STUKOWSKI A. Visualization and analysis of atomistic simulation data with ovito-the open visualization tool [J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(1): 015012. doi: 10.1088/0965-0393/18/1/015012 -






 下载:
下载: