Computational Analysis of RM Instability with Inverse Chevron Interface
-
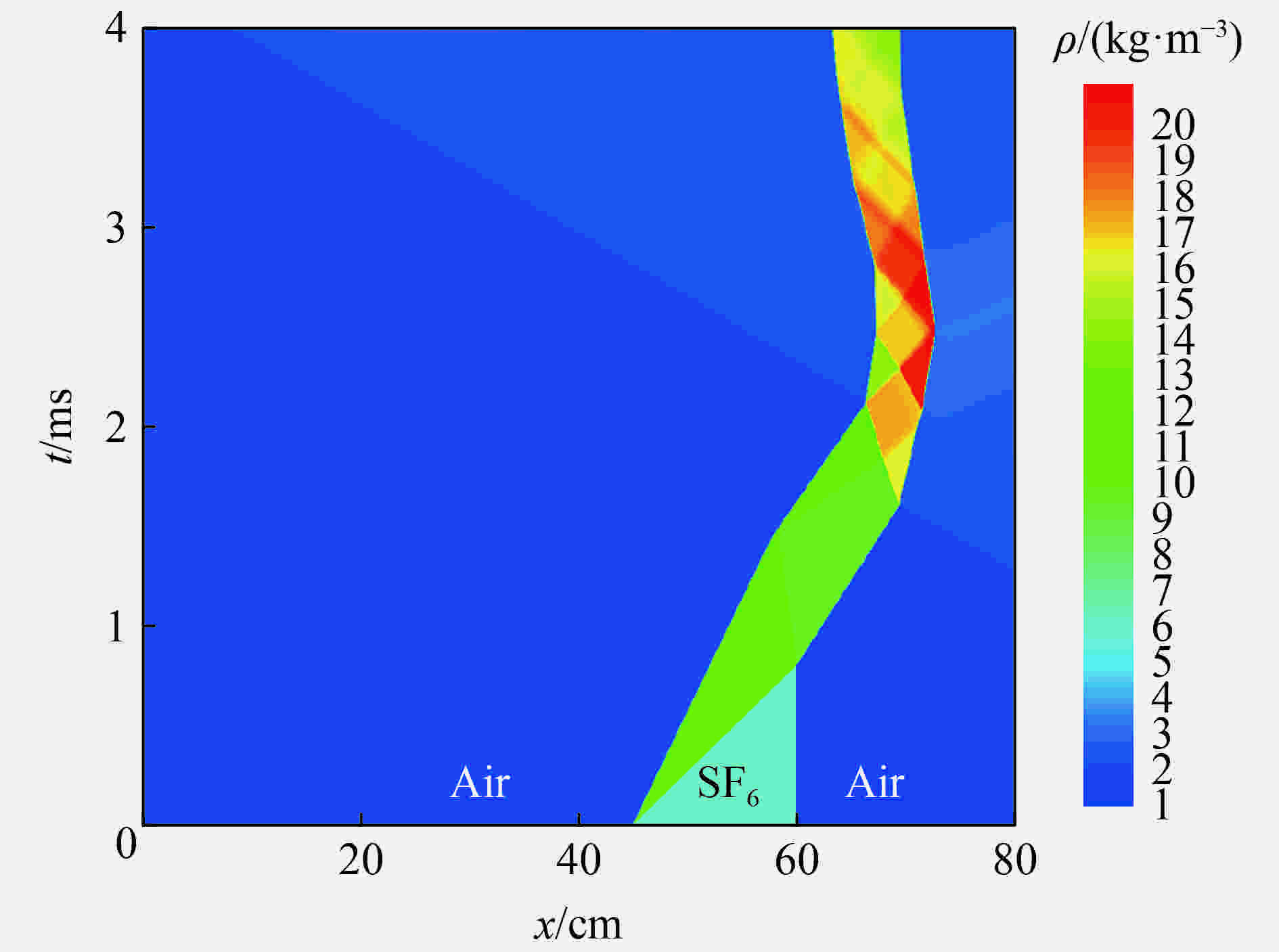
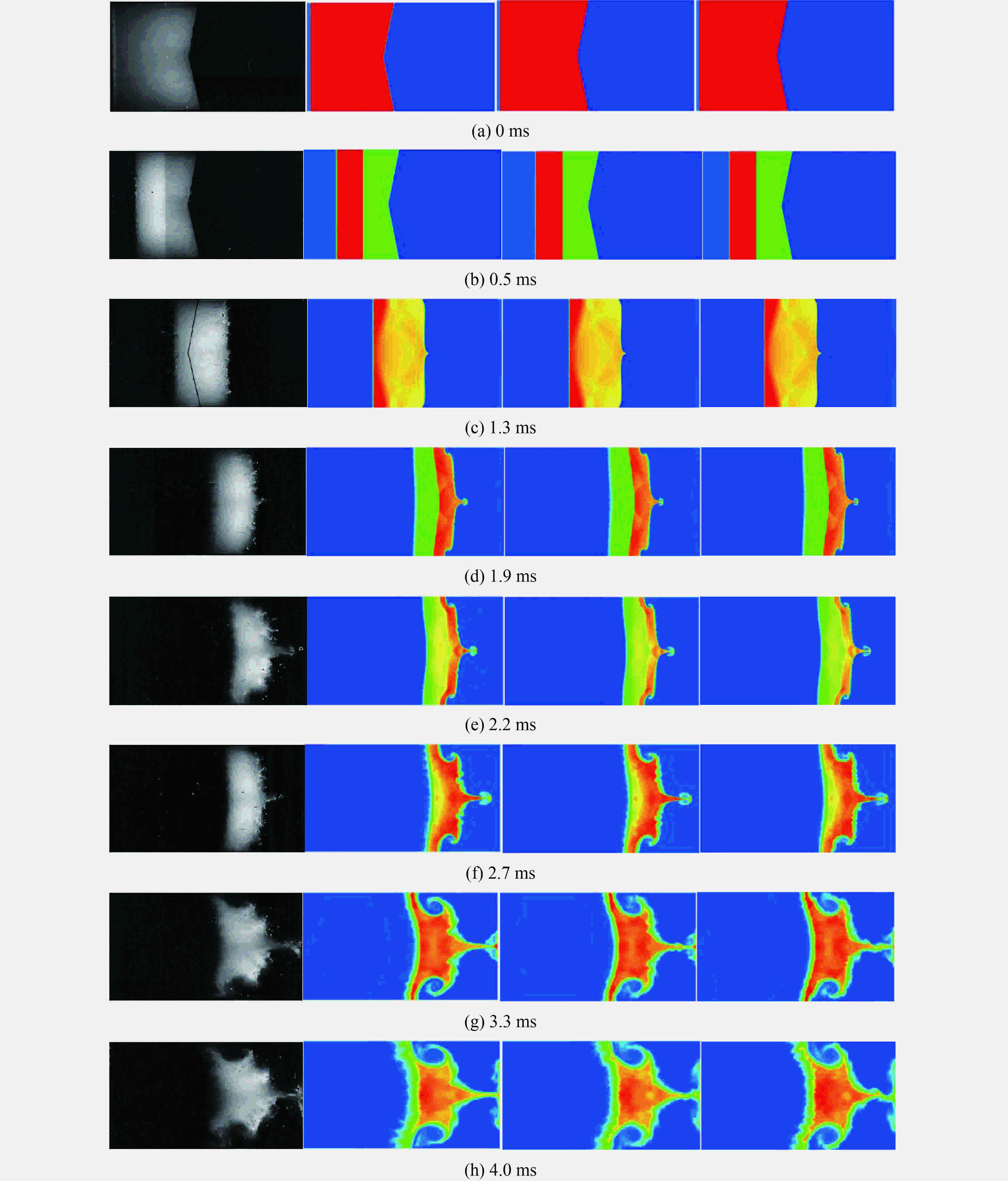
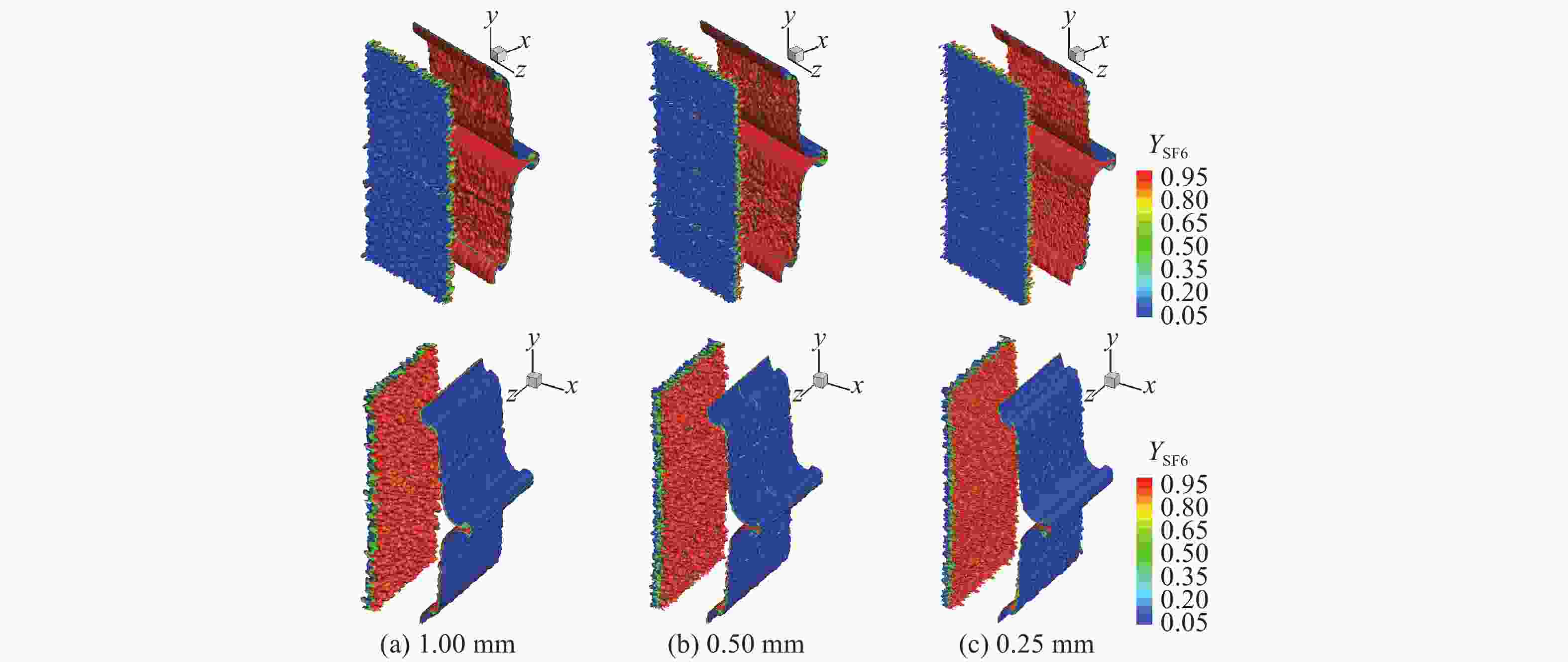
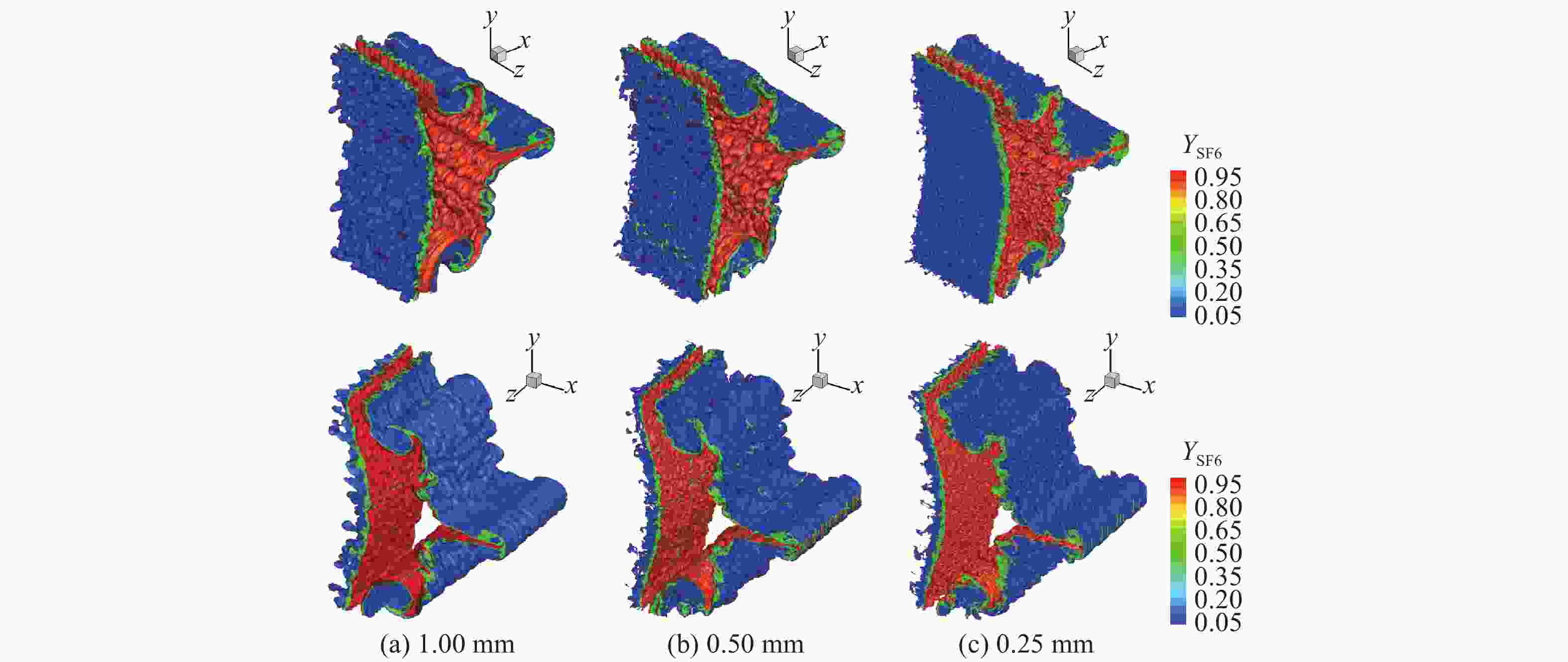
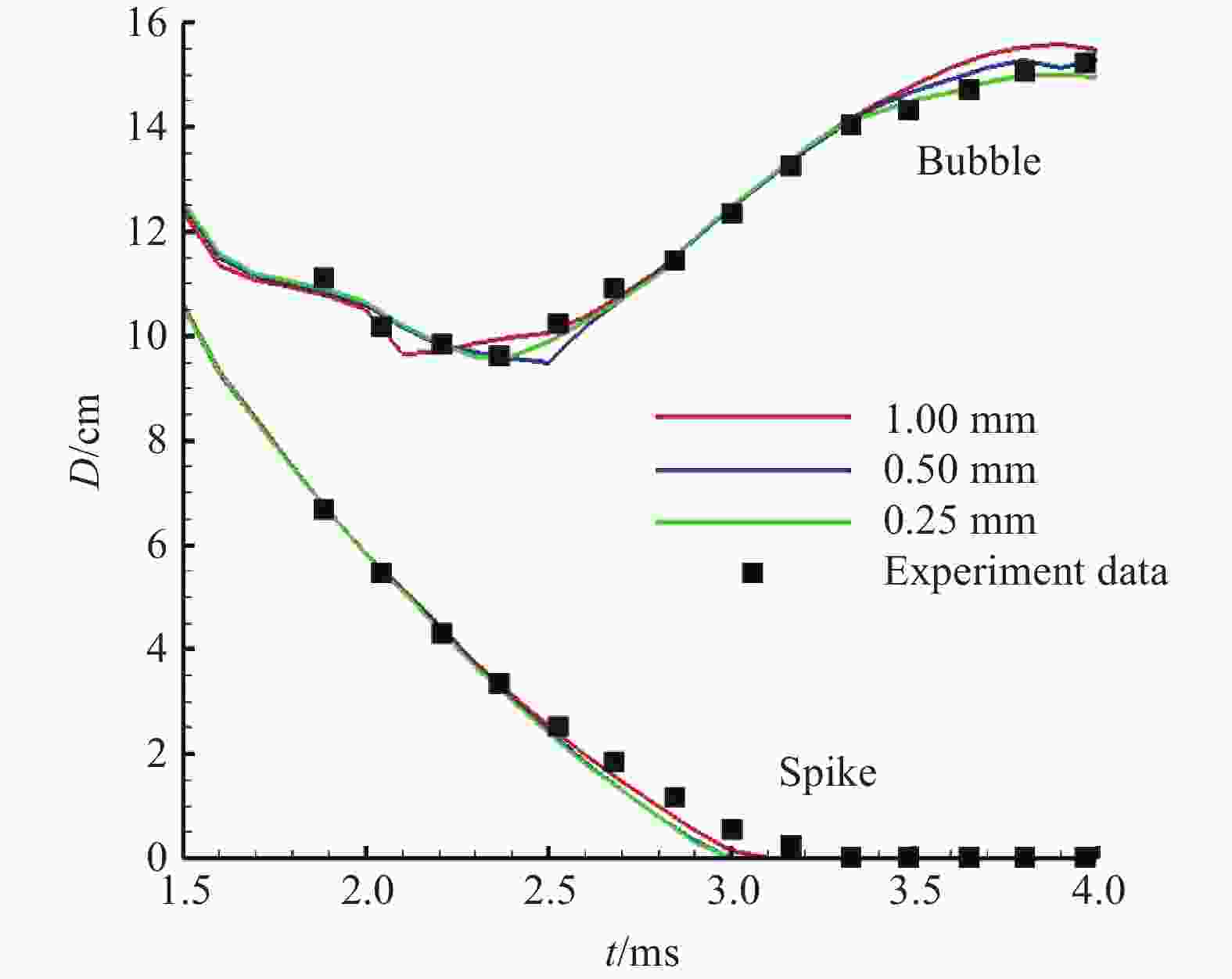
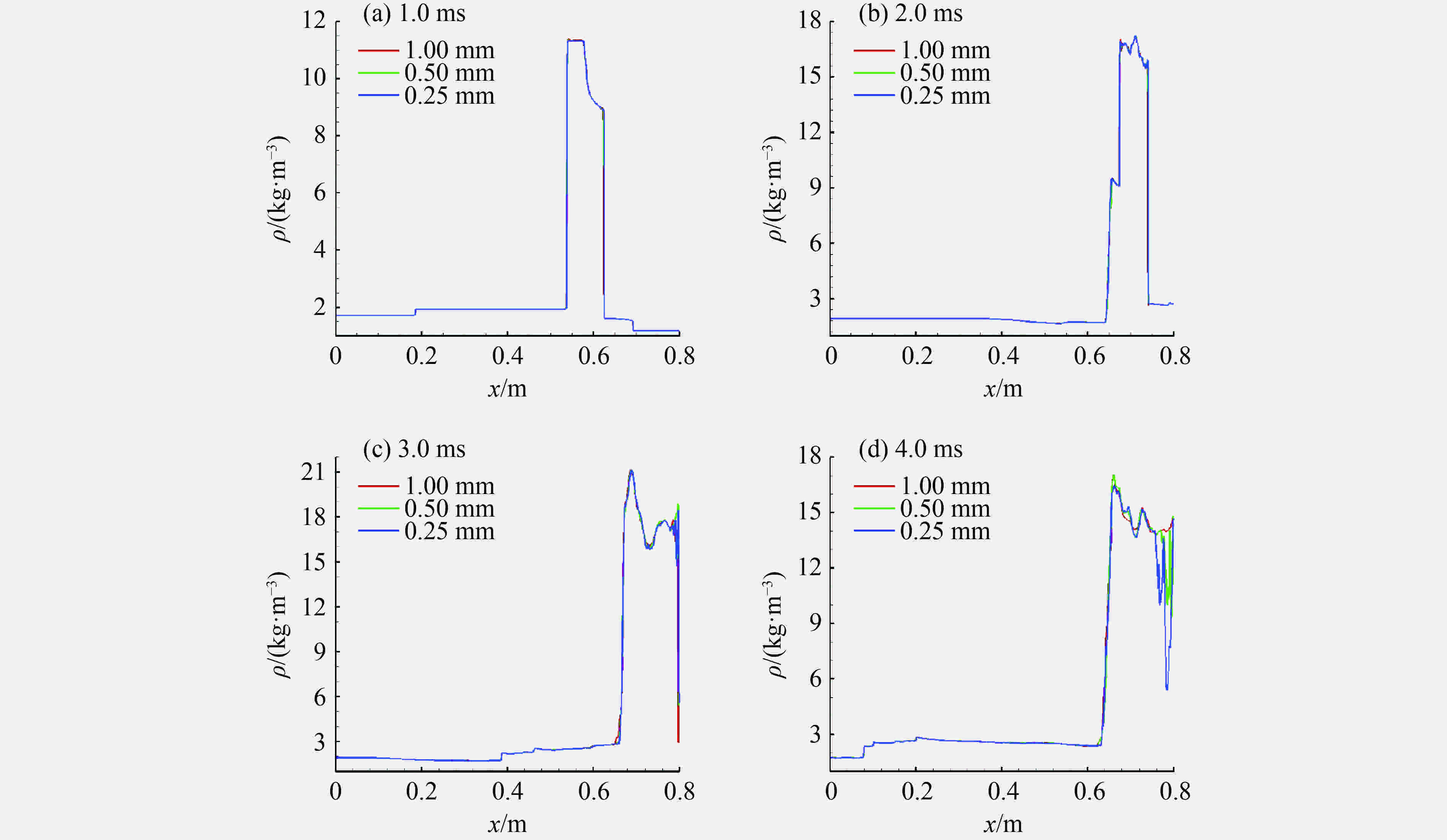
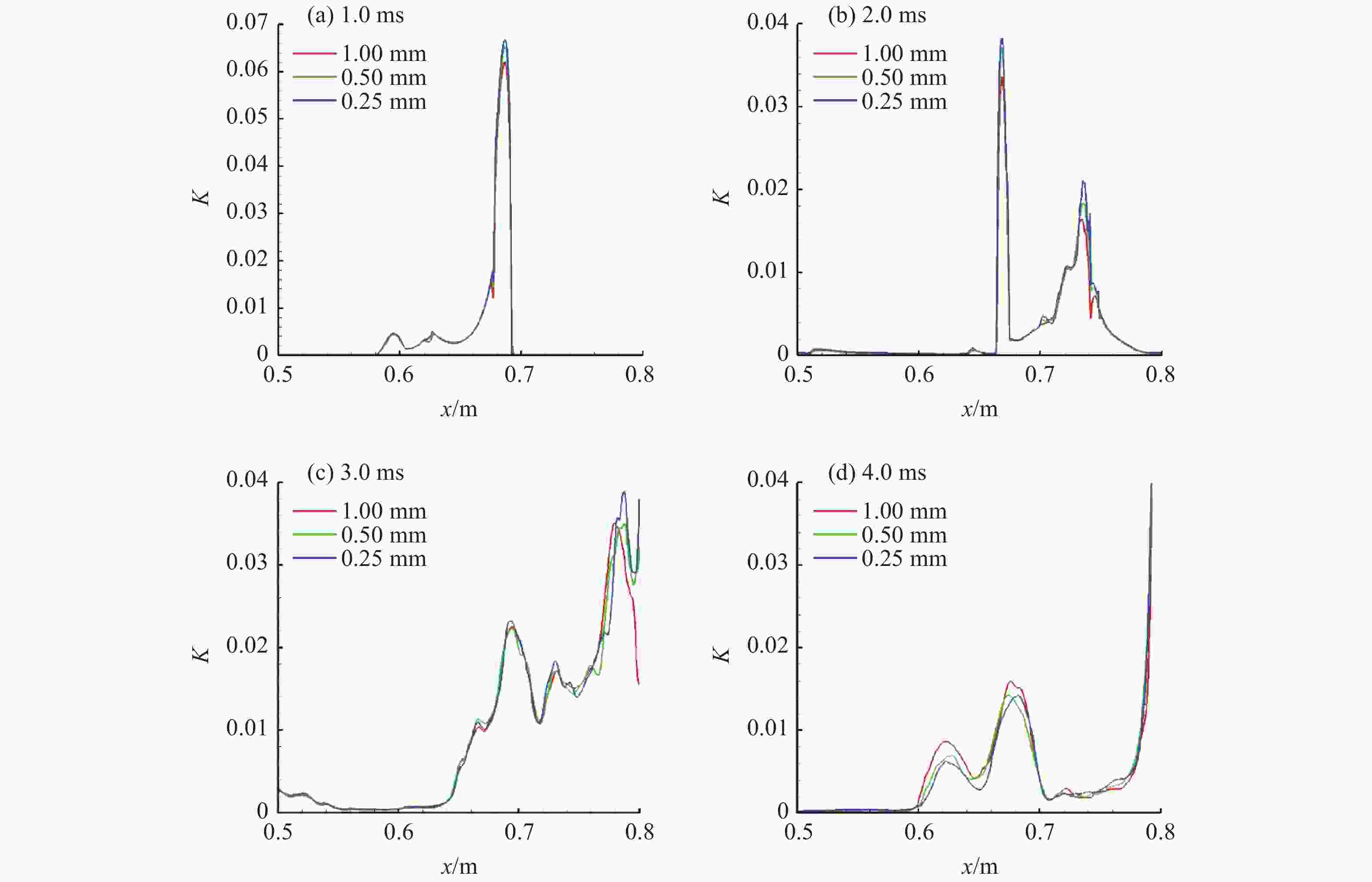
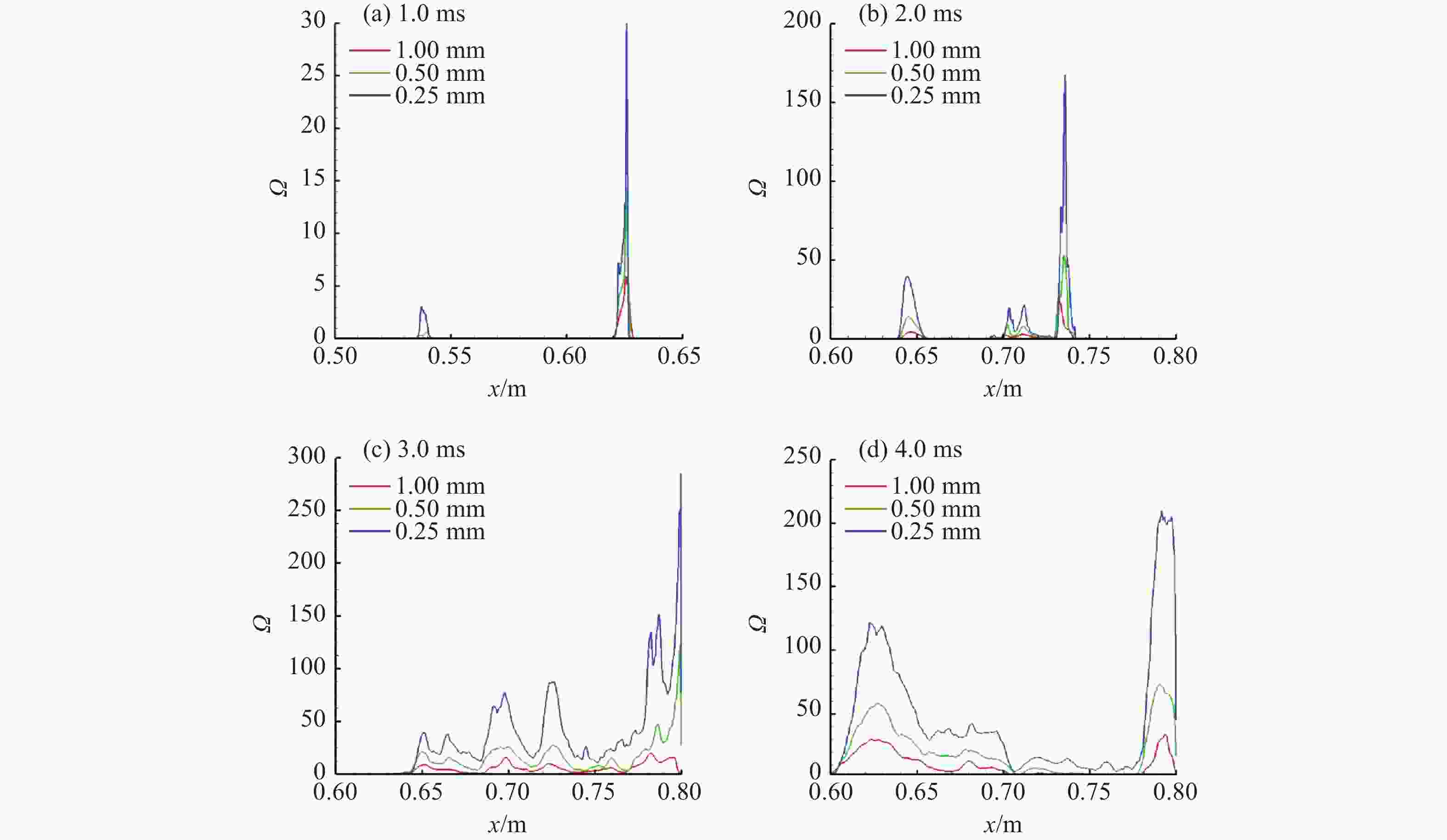
摘要: 利用可压缩多介质黏性流动和湍流大涡模拟代码(MVFT),在超算平台上对“反尖端”界面不稳定性及其诱发的湍流混合问题进行了大规模三维数值模拟分析。数值模拟结果清晰地显示了冲击波加载界面后分解产生的冲击波、稀疏波、压缩波及其在SF6气体中的运动和相互作用,以及波多次加载界面的复杂过程,波和界面的每一次作用都会加速湍流混合区的发展和物质混合。“反尖端”界面受冲击波加载后发生反相而形成典型的大尺度壁面气泡和中心轴尖钉结构,该大尺度结构基本确定了湍流混合区的平均几何特征和包络范围而不依赖计算网格。高分辨率的计算网格下,捕捉到了更精细的小尺度湍涡结构和更强的湍流脉动,显示了湍流混合区所具有的复杂结构和特征。Abstract: By using our in-house large-eddy simulation code, the MVFT (multi-viscous-flow and turbulence), we simulated the Richtmyer-Meshkov (RM) instability and turbulent mixed with the inverse chevron interface on a 3D large scale on the HPC (high performance computing) platform. The results revealed the propagations of the decomposed shock wave, the rarefaction wave, the compression wave and the interactions between the waves and the perturbed interface. Each impact of on the wave on the interface accelerates the evolution of the turbulent mixing zone and the materials’ mixing. The inverse chevron interface inverts its phase after the first transmitted shock wave in the SF6 zone hits it, then two wall bubbles and a centerline spike with large scale develop gradually. The averaged geometry feature and the envelop of turbulent mixing zone are determined by the large-scale wall bubbles and the centerline spike and are independent of the mesh. But with the higher grid resolution, more subtle small scale turbulent eddies and intense turbulent fluctuations are captured, characterizing the turbulent mixing zone as possessing a complex structure.
-
Key words:
- large-eddy simulation /
- interface instability /
- turbulent mixing /
- turbulent eddy
-
表 1 空气和SF6的初始参数
Table 1. Initial properties of air and SF6
Gas ρ/(kg·m–3) p/MPa γ μl/(Pa·s) Diffusion coefficient/(m2·s–1) SF6 5.97 0.1 1.09 1.474 6×10–5 0.97×10-5 Air 1.18 0.1 1.40 1.852 6×10–5 2.04×10–5 -
[1] RICHTMYER R D. Taylor instability in a shock acceleration of compressible of fluids [J]. Communications on Pure and Applied Mathematics, 1960, 13: 297–319. doi: 10.1002/(ISSN)1097-0312 [2] MESHKOV E E. Instability of the interface of two gases accelerated by a shock wave [J]. Fluid Dynamics, 1969, 4(5): 101–104. [3] CHANDRASEKHAR S. Hydrodynamic and hydromagnetic stability [M]. London: Oxford University, 1961. [4] 王涛, 柏劲松, 李平, 等. 再冲击载荷作用下流动混合的数值模拟 [J]. 爆炸与冲击, 2009, 29(3): 243–248 doi: 10.3321/j.issn:1001-1455.2009.03.004WANG T, BAI J S, LI P, et al. Numerical simulation of flow mixing impacted by reshock [J]. Explosion and Shock Waves, 2009, 29(3): 243–248 doi: 10.3321/j.issn:1001-1455.2009.03.004 [5] WANG T, BAI J S, LI P, et al. The numerical study of shock-induced hydrodynamic instability and mixing [J]. Chinese Physics B, 2009, 18(3): 1127–1135. doi: 10.1088/1674-1056/18/3/048 [6] BAI J S, LIU J H, WANG T, et al. Investigation of the Richtmyer-Meshkov instability with double perturbation interface in nonuniform flows [J]. Physical Review E, 2010, 81(2): 056302. [7] BAI J S, WANG B, WANG T, et al. Numerical simulation of the Richtmyer-Meshkov instability in initially nonuniform flows and mixing with reshock [J]. Physical Review E, 2012, 86(6): 066319. doi: 10.1103/PhysRevE.86.066319 [8] XIAO J X, BAI J S, WANG T. Numerical study of initial perturbation effects on Richtmyer-Meshkov instability in nonuniform flows [J]. Physical Review E, 2016, 94(1): 013112. doi: 10.1103/PhysRevE.94.013112 [9] LEINOV E, MALAMUD G, ELBAZ Y, et al. Experimental and numerical investigation of the Richtmyer–Meshkov instability under re-shock conditions [J]. Journal of Fluid Mechanics, 2009, 626: 449–475. doi: 10.1017/S0022112009005904 [10] THORNBER B, DRIKAKIS D, YOUNGS D L, et al. The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability [J]. Journal of Fluid Mechanics, 2010, 654: 99–139. doi: 10.1017/S0022112010000492 [11] LATINI M, SCHILLING O, DON W S. Richtmyer-Meshkov instability-induced mixing: initial conditions modeling, three-dimensional simulation and comparisons to experiment: UCRL-CONF-227160 [R]. Livermore: Lawrence Livermore National Laboratory, 2007. [12] SCHILLING O, LATINI M. High-order WENO simulations of three-dimensional reshocked Richtmyer–Meshkov instability to late times: dynamics, dependence on initial conditions, and comparisons to experimental data [J]. Acta Mathematica Scientia, 2010, 30(2): 595–620. doi: 10.1016/S0252-9602(10)60064-1 [13] MALAMUD G, LEINOV E, SADOT O, et al. Reshocked Richtmyer-Meshkov instability: numerical study and modeling of random multi-mode experiments [J]. Physics of Fluids, 2014, 26(8): 084107. doi: 10.1063/1.4893678 [14] MIKAELIAN K O. Testing an analytic model for Richtmyer–Meshkov turbulent mixing widths [J]. Shock Waves, 2015, 25(1): 35–45. doi: 10.1007/s00193-014-0537-0 [15] SI T, LONG T, ZHAI Z, et al. Experimental investigation of cylindrical converging shock waves interacting with a polygonal heavy gas cylinder [J]. Journal of Fluid Mechanics, 2015, 784: 225–251. doi: 10.1017/jfm.2015.581 [16] LIANG Y, DING J, ZHAI Z, et al. Interaction of cylindrically converging diffracted shock with uniform interface [J]. Physics of Fluids, 2017, 29(8): 086101. doi: 10.1063/1.4997071 [17] HILL D J, PANTANO C, PULLIN D I. Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock [J]. Journal of Fluid Mechanics, 2006, 557: 29–61. doi: 10.1017/S0022112006009475 [18] GRINSTEIN F F, GOWARDHAN A A, WACHTOR A J. Simulations of Richtmyer–Meshkov instabilities in planar shock-tube experiments [J]. Physics of Fluids, 2011, 23(3): 034106. doi: 10.1063/1.3555635 [19] WEBER C, HAEHN N, OAKLEY J, et al. Turbulent mixing measurements in the Richtmyer-Meshkov instability [J]. Physics of Fluids, 2012, 24(7): 074105. doi: 10.1063/1.4733447 [20] TRITSCHLER V K, OLSON B J, LELE S K, et al. On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface [J]. Journal of Fluid Mechanics, 2014, 755: 429–462. doi: 10.1017/jfm.2014.436 [21] WANG T, BAI J S, LI P, et al. Large-eddy simulations of the multi-mode Richtmyer–Meshkov instability and turbulent mixing under reshock [J]. High Energy Density Physics, 2016, 19: 65–75. doi: 10.1016/j.hedp.2016.03.001 [22] WANG T, TAO G, BAI J, et al. Dynamical behavior of the Richtmyer–Meshkov instability-induced turbulent mixing under multiple shock interactions [J]. Canadian Journal of Physics, 2017, 95(8): 671–681. doi: 10.1139/cjp-2016-0633 [23] MOHAGHAR M, CARTER J, MUSCI B, et al. Evaluation of turbulent mixing transition in a shock-driven variable-density flow [J]. Journal of Fluid Mechanics, 2017, 831: 779–825. doi: 10.1017/jfm.2017.664 [24] BANERJEE A, GORE R A, ANDREWS M J. Development and validation of a turbulent-mix model for variable-density and compressible flows [J]. Physical Review E, 2010, 82(4): 046309. doi: 10.1103/PhysRevE.82.046309 [25] CABOT W H, COOK A W. Reynolds number effects on Rayleigh–Taylor instability with possible implications for type-Ia supernovae [J]. Nature Physics, 2006, 2(8): 562–568. doi: 10.1038/nphys361 [26] VREMAN A W. An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications [J]. Physics of Fluids, 2004, 16(10): 3670–3681. doi: 10.1063/1.1785131 [27] HOLDER D A, BARTON C J. Shock tube Richtmyer-Meshkov experiments: inverse chevron and half height [C]// Proceedings of the 9th International Workshop on Physics of Compressible Turbulent Mixing. Cambridge, UK, 2004. -






 下载:
下载: