Dynamic Response and Optical Properties of PMMA under Shock Compression
-
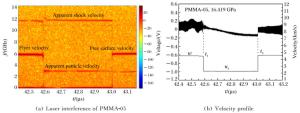
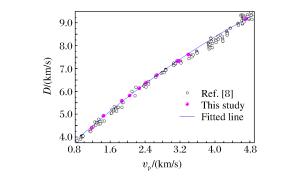
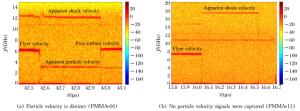
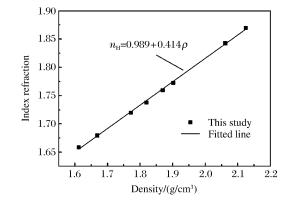
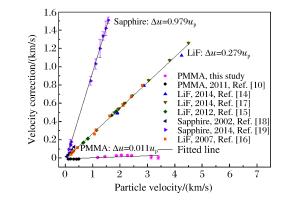
摘要: 利用二级轻气炮测量了聚甲基丙烯酸甲酯(Polymethylmethacrylate,PMMA)在一维平面冲击压缩条件下的响应和光学特性。采用全光纤激光干涉测试技术(DPS)测量样品在冲击加载下的界面粒子速度和冲击波速度,获得了PMMA材料在冲击压力6~50 GPa区间内的高精度冲击Hugoniot数据,冲击波速度不确定度小于1%。同时获得了冲击压缩条件下PMMA样品材料的高压折射率与密度的变化关系以及界面粒子速度修正系数,并实时观测到了PMMA材料中的表观冲击波速度剖面,讨论了冲击波速度剖面与真实冲击波速度的关系。Abstract: Symmetric plate impact experiments were performed using a two-stage light gas gun to investigate the dynamic response and optical properties of polymethylmethacrylate (PMMA) under shock loading.The particle velocity of the flyer/sample interface, the shock velocity, and the refractive index of the sample were measured using a Doppler pin system (DPS).The measurements produced accurate Hugoniot data for PMMA, with the uncertainty of the shock velocity below 1%.The velocity correction at 1 550 nm of the wavelength under shock pressures ranging from 6 to 50 GPa was also obtained.The relationship between the refractive index and the density under shock compression was deduced from the measurements.Moreover, the shock velocity was distinctly captured by DPS and its relationship with the actual shock velocity was examined.
-
Key words:
- PMMA /
- shock compression /
- Hugoniot /
- Doppler pin system (DPS) /
- velocity correction
-
表 1 PMMA实验结果
Table 1. Experimental results of PMMA
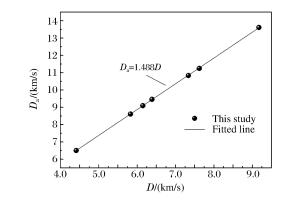
Exp. No. w/(km/s) D/(km/s) Da/(km/s) up/(km/s) ua/(km/s) Δu/(km/s) p/(GPa) nH PMMA-01(a) 2.353 4.41±0.01 6.508 1.177±0.003 1.185±0.004 0.008±0.005 6.13±0.02 1.66 PMMA-02(a) 2.884 4.94±0.01 (c) 1.442±0.003 1.461±0.002 0.019±0.004 8.41±0.04 1.68 PMMA-03(a) 3.724 5.59±0.01 (c) 1.862±0.005 1.890±0.005 0.028±0.007 12.30±0.05 1.72 PMMA-04(a) 4.083 5.82±0.01 8.613 2.042±0.005 2.076±0.002 0.034±0.005 14.05±0.06 1.74 PMMA-05(a) 4.523 6.15±0.01 9.100 2.262±0.006 2.292±0.006 0.030±0.008 16.42±0.07 1.76 PMMA-06(a) 4.836 6.38±0.03 9.463 2.418±0.006 2.447±0.002 0.029±0.006 18.23±0.09 1.77 PMMA-07(b) 3.170 6.72±0.01 (c) 2.665±0.015 (d) - 21.14±0.14 - PMMA-08(b) 3.754 7.33±0.01 10.839 3.130±0.017 3.144±0.014 0.014±0.022 27.11±0.17 1.84 PMMA-09(b) 3.795 7.34±0.01 (c) 3.165±0.018 (d) - 27.42±0.18 - PMMA-10(b) 4.075 7.62±0.02 11.250 3.387±0.019 3.396±0.006 0.009±0.020 30.47±0.20 1.87 PMMA-11(b) 5.731 9.17±0.03 13.613 4.694±0.027 (e) - 50.84±0.35 - -
[1] RENHART W D, CHHABILDAS L C, VOGLER T J.Investigating phase transitions and strength in single-crystal sapphire using shock-reshock loading techniques [J].Int J Impact Eng, 2006, 33(1):655-669. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a7ca65623b2ed81de666cf9de8c9fbfa [2] PELISSIER J L, PARTOUCHE-SEBBAN D.Pyrometry measurements on shock-heated bismuth using PMMA and sapphire windows [J].Physica B, 2005, 364(1):14-28. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7a925e72127f8da8b27e71a6b8c04921 [3] CHHABILDAS L C, ASAY J R.Rise-time measurements of shock transitions in aluminum, copper, and steel [J].J Appl Phys, 1979, 50(4):2749-2756. doi: 10.1063/1.326236 [4] BARKER L M, HOLLENBACH R E.Laser interferometer for measuring high velocities of any reflecting surface [J].J Appl Phys, 1972, 43(11):4669-4675. doi: 10.1063/1.1660986 [5] WENG J D, TAN H, HU S L, et al.New all-fiber velocimeter [J].Rev Sci Instrum, 2005, 76(9):093301. doi: 10.1063/1.2008989 [6] WENG J D, TAN H, WANG X, et al.Optical-fiber interferometer for velocity measurements with picosecond resolution [J].Appl Phys Lett, 2006, 89(11):111101. doi: 10.1063/1.2335948 [7] WENG J D, WANG X, MA Y, et al.A compact all-fiber displacement interferometer for measuring the foil velocity driven by laser [J].Rev Sci Instrum, 2008, 79(11):113101. doi: 10.1063/1.3020700 [8] STRAND O T, GOOSMAN D R, MAREINEZ C, et al.Compact system for high-speed velocimetry using heterodyne techniques [J].Rev Sci Instrum, 2006, 77(8):083108. doi: 10.1063/1.2336749 [9] MARSH S P.LASL shock Hugoniot data [M].Berkeley, CA:University of California Press, 1980:446-451. [10] BARKER L M, HOLLENBACH R E.Shock wave studies of PMMA, fused silicon, and sapphire [J].J Appl Phys, 1970, 41(10):4208-4226. doi: 10.1063/1.1658439 [11] CHAPMAN D J, EAKINS D E, WILLIAMSON D M, et al.Index of refraction measurements and window corrections for PMMA under shock compression [C]//ELERT M L, BUTTLER W T, BORG J P, et al.Shock Compression of Condensed Matter-2011.New York: AIP, 2012. [12] 经福谦.实验物态方程导引[M].第2版.北京:科学出版社, 1999.JING F Q.Introduction to experimental equation of state [M].2nd ed.Beijing:Science Press, 1999. [13] 王为, 陈宏, 王翔.紧凑型全光纤内弹道弹速测量系统[J].应用光学, 2011, 32(4):723-729. doi: 10.3969/j.issn.1002-2082.2011.04.026WANG W, CHEN H, WANG X.Compact all fiber interior ballistic projectile velocity measurement system [J].J Appl Optics, 2011, 32(4):723-729. doi: 10.3969/j.issn.1002-2082.2011.04.026 [14] JENSEN B J, HOLTKAMP D B, RIGG P A, et al.Accuracy limits and window corrections for photon Doppler velocimetry [J].J Appl Phys, 2007, 101(1):013523. doi: 10.1063/1.2407290 [15] 赵万广, 周显明, 李加波, 等.LiF单晶的高压折射率及窗口速度的修正[J].高压物理学报, 2014, 28(5):571-576. http://www.gywlxb.cn/CN/abstract/abstract1746.shtmlZHAO W G, ZHOU X M, LI J B, et al.Refractive index of LiF single crystal at high pressure and its window correction [J].Chinese Journal of High Pressure Physics, 2014, 28(5):571-576. http://www.gywlxb.cn/CN/abstract/abstract1746.shtml [16] 李雪梅, 俞宇颖, 张林, 等.〈100〉 LiF的低压冲击响应和1 550 nm波长下的窗口速度修正[J].物理学报, 2012, 61(15):156202. doi: 10.7498/aps.61.156202LI X M, YU Y Y, ZHANG L, et al.Elastic-plastic response of shocked 〈100〉 LiF and its window correction at 1 550 nm wavelength [J].Acta Phys Sin, 2012, 61(15):156202. doi: 10.7498/aps.61.156202 [17] 马云, 李泽仁, 胡绍楼, 等.用作VISAR窗口的LiF晶体折射率变化修正因子[J].高压物理学报, 2007, 21(4):397-400. doi: 10.3969/j.issn.1000-5773.2007.04.011MA Y, LI Z R, HU S L, et al.LiF window corrections for VISAR [J].Chinese Journal of High Pressure Physics, 2007, 21(4):397-400. doi: 10.3969/j.issn.1000-5773.2007.04.011 [18] RIGG P A, KNUDSON M D, SCHARFF R J, et al.Determining the refractive index of shocked[100] lithium fluoride to the limit of transmissibility [J].J Appl Phys, 2014, 116(3):033515. doi: 10.1063/1.4890714 [19] SETCHELL R E.Refractive index of sapphire at 532 nm under shock compression and release [J].J Appl Phys, 2002, 91(5):2833-2841. doi: 10.1063/1.1446219 [20] CAO X X, LI J B, LI J, et al.Refractive index of r-cut sapphire under shock pressure range 5 to 65 GPa [J].J Appl Phys, 2014, 116(9):093516. doi: 10.1063/1.4894854 -







 下载:
下载: