Resistance Performance of Grooved Metal Target Subjected to Projectile Impact
doi: 10.11858/gywlxb.2017.02.002
-
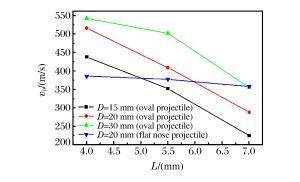
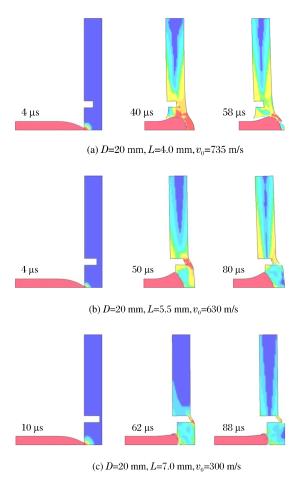
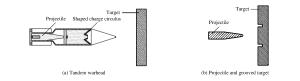
摘要: 采用弹道实验和数值模拟的方法研究了带环形预裂槽的金属靶在射弹冲击下的毁伤模式和防护性能,分析了弹头形状、预裂槽直径及深度等因素对靶板防护性能的影响。结果表明:对带有环形预裂槽的金属靶板,存在两种主要毁伤模式,即环形槽内部的侵彻和环形槽底的冲击断裂;临界毁伤速度与毁伤模式密切相关,随着环形槽深度的增大或半径的变小,临界毁伤速度变小;与尖头弹相比,平头弹的临界毁伤速度更小;微观分析表明,在射弹冲击作用下,环形槽底部产生绝热剪切带,更容易形成充塞剪切破坏。Abstract: The damage modes and resistance performance of the annular pre-cut metal target impacted by the projectile were studied by experiments and numerical simulation.Influences of the projectile nose shape, the diameter as well as the depth of the annular groove on the resistance performance of the target were analyzed.The results show that there exist two kinds of damage modes for the target with an annular groove, one being the penetration of the inner part of the groove and the other the fracture along the bottom of the annular groove.The critical damage velocity (CDV) is closely related to the damage modes of the target.Generally, the grooved target was easier to be damaged than the intact one.The CDV decreases with the increase of the annular groove depth while it goes up with the increase of the annular groove diameter.Compared with the oval nose projectile, the CDV of the target is smaller for the flat nose projectile.The microscopic analysis shows that when the adiabatic shear band is formed inside the target, the plug is easier to be formed and the target is easier to be damaged.
-
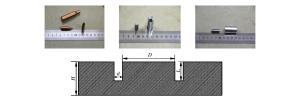
Table 1. Various experimental conditions
Projectile D/(mm) L/(mm) Projectile D/(mm) L/(mm) Oval projectile 15 4.0
5.5
7.0Oval projectile 30 4.0
5.5
7.020 4.0
5.5
7.0Flat nose projectile 20 4.0
5.5
7.0Material A/
(MPa)B/
(MPa)N C M D1 D2 D3 D4 D5 304L steel 792 510 0.260 0.014 1.03 -0.8 2.10 -0.50 0.002 0.61 45 steel 507 320 0.064 0.280 1.06 0.1 0.76 1.57 0.085 -0.84 Material ρ0/(g/cm3) S1/(MPa) S2/(MPa) S3/(MPa) γ0 a 304L steel 7.83 164 294 500 1.16 0.46 45 steel 7.81 153 271 483 1.12 0.44 Table 4. Numerical simulation results of damage modes and CDV
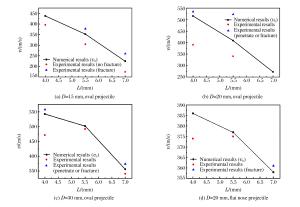
Projectile D/(mm) L/(mm) v0/(m/s) Damage mode Oval projectile ∞ 0 624 Penetrate 15 4.0
5.5
7.0438
352
225Penetrate
Penetrate
Fracture20 4.0
5.5
7.0516
409
288Penetrate
Fracture
Fracture30 4.0
5.5
7.0543
502
356Penetrate
Penetrate
FractureFlat nose projectile 20 4.0
5.5
7.0386
377
358Penetrate
Fracture
FractureTable 5. Experimental results
Projectile D/(mm) L/(mm) Mass/(g) v/(m/s) Damage model Oval projectile 15 4.0
5.5
5.5
7.0
7.09.65
9.65
9.65
9.65
9.65396.0
378.0
305.0
260.0
174.5No penetrate
Fracture
No fracture
Fracture
No fracture20 4.0
4.0
5.5
5.59.65
9.65
9.65
9.65390.6
535.0
523.0
341.0No penetrate
Penetrate
Fracture
No fracture30 4.0
4.0
5.5
7.0
7.09.65
9.65
9.65
9.65
9.65558.0
471.7
492.0
341.0
374.0Penetrate
No penetrate
Penetrate
No fracture
Critical fractureFlat nose projectile 20 4.0
5.5
7.07.81
7.81
7.81374.0
375.0
363.0No fracture
Critical fracture
Fracture -
[1] 董立松, 刘宁, 辛士进, 等.高硬度装甲钢抗弹性能及其机理研究[J].兵器材料科学与工程, 2010, 33(2):76-78. doi: 10.3969/j.issn.1004-244X.2010.02.022DONG L S, LIU N, XIN S J, et al.Study on ballistic performance and mechanism of high hardness armor steel[J].Ordnance Material Science and Engineering, 2010, 33(2):76-78. doi: 10.3969/j.issn.1004-244X.2010.02.022 [2] 李晓源, 时捷, 董瀚.不同强度的40CrNi2Mo钢抗弹性能研究[J].兵器材料科学与工程, 2008, 31(1):14-18. doi: 10.3969/j.issn.1004-244X.2008.01.004LI X Y, SHI J, DONG H.Research on ballistic behavior of 40CrNi2Mo steel targets with different strength[J].Ordnance Material Science and Engineering, 2008, 31(1):14-18. doi: 10.3969/j.issn.1004-244X.2008.01.004 [3] 时捷, 董瀚, 王琪, 等.硬度对装甲钢板抗弹性能的影响[J].钢铁研究学报, 2000, 12(3):36-41. doi: 10.3321/j.issn:1001-0963.2000.03.009SHI J, DONG H, WANG Q, et al.Influence of hardness on the ballistic behavior of armor steel plate[J].Journal of Iron and Steel Research, 2000, 12(3):36-41. doi: 10.3321/j.issn:1001-0963.2000.03.009 [4] SANGOY L, MEUNIER Y, PONT G.Steels for ballistic protection[J].Israel J Technol, 1988, 24:319-326. http://cn.bing.com/academic/profile?id=8e9783ddda52b532c0590c03189e82d6&encoded=0&v=paper_preview&mkt=zh-cn [5] 张清华, 李伯龙, 聂祚仁, 等.高速冲击下2519A-T87铝合金微观组织研究[J].科学技术与工程, 2011, 11(15):3413-3416. doi: 10.3969/j.issn.1671-1815.2011.15.012ZHANG Q H, LI B L, NIE Z R, et al.Microstructure evolution of 2519A-T87 during projectile impact[J].Science Technology and Engineering, 2011, 11(15):3413-3416. doi: 10.3969/j.issn.1671-1815.2011.15.012 [6] BALAKRISHNAN M, BALASUBRAMANIAN V, REDDY G M.Micro structural analysis of ballistic tests on welded armor steel joints[J].Metallography, Microstructure & Analysis, 2013, 2:125-139. doi: 10.1007/s13632-013-0069-5 [7] DUAN Z Q, LI S X, HUANG D W.Microstructures and adiabatic shear band formed by ballistic impact in steels and tungsten alloy[J].Fatigue Fract Eng Mater Struct, 2003, 26:1119-1126. doi: 10.1046/j.1460-2695.2003.00705.x [8] ZOU D L, ZHEN L, XU C Y, et al.Characterization of adiabatic shear bands in AM60B magnesium alloy under ballistic impact[J].Mater Charact, 2011, 62(5):496-502. doi: 10.1016/j.matchar.2011.03.003 [9] ATAPEK S H, KARAGOZ S.Ballistic impact behavior of a tempered bainitic steel against 7.62 mm armour piercing projectile[J].Defence Sci J, 2011, 61(1):81-87. doi: 10.14429/dsj [10] HU C J, LEE P Y, CHEN J S.Ballistic performance and microstructure of modified rolled homogeneous armor steel[J].Journal of the Chinese Institute of Engineers, 2002, 25(1):99-107. doi: 10.1080/02533839.2002.9670684 [11] SASTRY Y B S, BUDARAPU PATTABHI R, KRISHNA Y, et al.Studies on ballistic impact of the composite panels[J].Theor Appl Fract Mech, 2014, 72:2-12. doi: 10.1016/j.tafmec.2014.07.010 [12] 李金泉, 黄德武, 段占强, 等.穿甲侵彻过程中靶板内绝热剪切带特性及形成原因分析[J].兵工学报, 2005, 26(1):60-63. http://d.old.wanfangdata.com.cn/Periodical/bgxb200501013LI J Q, HUANG D W, DUAN Z Q, et al.Analysis on adiabatic shear band characteristic and cause of formation in process of penetration in armor[J].Acta Armamentarii, 2005, 26(1):60-63. http://d.old.wanfangdata.com.cn/Periodical/bgxb200501013 [13] 段春争, 王敏杰.30CrNi3MoV钢锯齿形切屑中绝热剪切带的微结构特征[J].机械工程材料, 2004, 28(10):16-19. doi: 10.3969/j.issn.1000-3738.2004.10.006DUAN C Z, WANG M J.Microstructure characteristic of the adiabatic shear bands in serrated chips of 30CrNi3MoV steel[J].Materials for Mechanical Engineering, 2004, 28(10):16-19. doi: 10.3969/j.issn.1000-3738.2004.10.006 [14] WITTMAN C L, MEYERS M A, PA H R.Observation of an adiabatic shear band in AISI4340 steel by high-voltage transmission electron microscopy[J].Metallurg Trans A, 1990, 21(2):707-716. doi: 10.1007/BF02671941 [15] ODESHI A G, AL-AMEERI S, BASSIM M N.Effect of high strain rate on plastic deformation of low allow steel subjected to ballistic impact[J].J Mater Process Tech, 2005, 162/163:385-391. doi: 10.1016/j.jmatprotec.2005.02.157 [16] ZHOU N, WANG J X, YANG R.Damage mechanism and anti-penetration performance of multi-layered explosively welded plates impacted by spherical projectile[J].Theor Appl Fract Mech, 2012, 60(1):23-30. http://www.sciencedirect.com/science/article/pii/S0167844212000572 [17] 陈刚, 陈忠富, 徐伟芳, 等.45钢的J-C损伤失效参量研究[J].爆炸与冲击, 2007, 27(2):131-135. doi: 10.3321/j.issn:1001-1455.2007.02.007CHEN G, CHEN Z F, XU W F, et al.Investigation on the J-C ductile fracture parameters of 45 steel[J].Explosion and Shock Waves, 2007, 27(2):131-135. doi: 10.3321/j.issn:1001-1455.2007.02.007 -
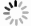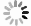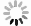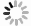





 下载:
下载: