爆炸复合边界效应的数值模拟

缪广红; 王章文; 李亮; 江向阳; 刘文震; 程扬帆; 汪泉; 余勇; 马宏昊; 沈兆武

doi:10.11858/gywlxb.2017.01.014

爆炸复合边界效应的数值模拟

doi: 10.11858/gywlxb.2017.01.014

1.
安徽理工大学力学与光电物理学院，安徽淮南 232001
2.
中国科学技术大学近代力学系，安徽合肥 230027
3.
安徽理工大学化学工程学院，安徽淮南 232001

基金项目:

国家自然科学基金 11502001

国家自然科学基金 11602001

安徽省自然科学基金 1608085QA15

安徽理工大学博士基金

安徽理工大学大学生创新创业训练计划项目

详细信息

作者简介:
缪广红(1985-), 男, 博士, 讲师, 主要从事含能材料、爆炸复合及爆炸力学相关研究.E-mail:miaogh@mail.ustc.edu.cn

中图分类号: O347.1;TG456.6
计量
- 文章访问数: 7332
- HTML全文浏览量: 2631
- PDF下载量: 142
出版历程
- 收稿日期: 2016-06-08
- 修回日期: 2016-08-08

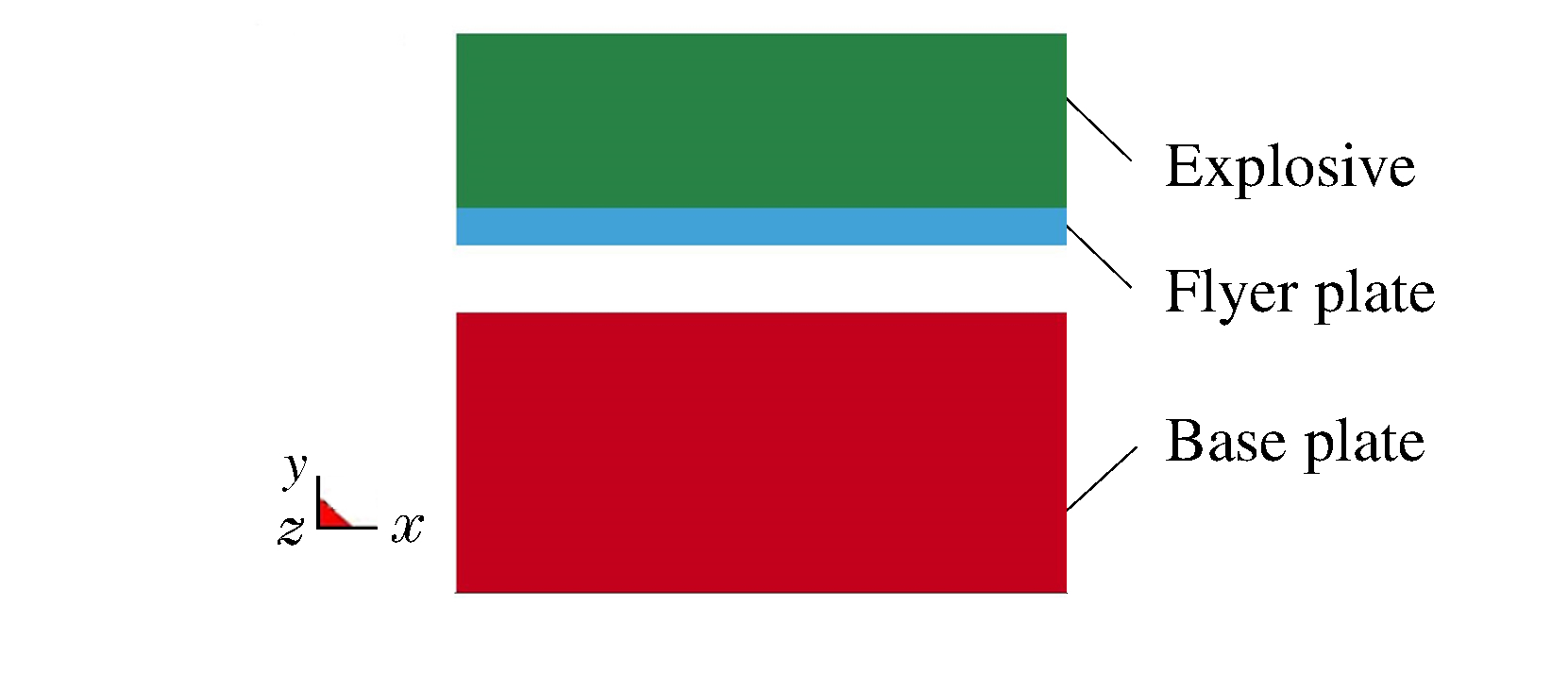
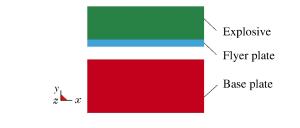
Numerical Simulation of Boundary Effect in Explosive Cladding

1.
School of Mechanics and Optoelectronic Physics, Anhui University ofScience and Technology, Huainan 232001, China
2.
Department of Modern Mechanics, University of Science andTechnology of China, Hefei 230027, China
3.
School of Chemical Engineering, Anhui University ofScience and Technology, Huainan 232001, China

摘要

摘要: 借助动力学分析软件ANSYS/LS-DYNA，运用光滑粒子流体动力学(SPH)方法，对爆炸复合边界效应进行了二维数值模拟。模拟结果再现了爆炸复合过程中的射流现象和边界效应。研究结果表明，爆炸复合边界效应的产生原因并非是边界处的冲击能量过剩，在基-复板碰撞之前，断裂就已经产生。采用SPH方法对爆炸复合边界效应进行模拟研究具有一定的科学价值。
- 爆炸力学 /
- 爆炸复合 /
- 边界效应 /
- 光滑粒子流体动力学方法 /
- 数值模拟
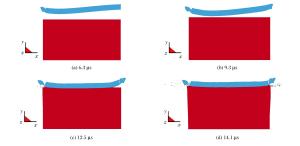
Abstract: The dynamic analysis software ANSYS/LS-DYNA was used in combination with smoothed particle hydrodynamics (SPH) method to simulate the boundary effect in explosive cladding.The two-dimensional simulation results reproduced the phenomenon of metal jet and boundary effect and were consistent with the production practice of explosive cladding.The simulated results also revealed that the fracture of the flyer plate occurs before the collision.Therefore, it can be drawn that the boundary effect here is not due to the excessive energy at the edge area.It is valuable to investigate the boundary effect in explosive cladding with SPH method.
- mechanics of explosion /
- explosive cladding /
- boundary effect /
- smoothed particle hydrodynamics method /
- numerical simulation

HTML全文

图 1 计算模型

Figure 1. Calculation model

下载: 全尺寸图片幻灯片

图 2 不同时刻爆炸复合过程中复板的飞行姿态

Figure 2. Flight attitudes of flyer plate at different time

下载: 全尺寸图片幻灯片

表 1 乳化炸药的JWL状态参数

Table 1. JWL equation-of-state parameters of emulsion explosives

Density/(g/cm³)	D/(km/s)	A/(GPa)	B/(GPa)	R₁	R₂	ω	E₀/(kJ/cm³)
1.12	4.51	326.42	5.81	5.80	1.56	0.57	3.32

下载: 导出CSV

表 2 Q235钢的Johnson-Cook模型参数

Table 2. Johnson-Cook parameters of Q235 steel

Density/(g/cm³)	A_m/(GPa)	B_m/(GPa)	C_m	n	m	T_melt/(K)	T_room/(K)
7.83	0.792	0.510	0.014	0.26	1.03	1 793	294

下载: 导出CSV

参考文献(12)

[1]	李选明, 焦永刚.TA10合金厚板与钢爆炸焊接边界效应的产生与消除[J].稀有金属快报, 1999(10):5-6. http://www.cnki.com.cn/Article/CJFDTOTAL-XJKB199910004.htm
[2]	郑远谋.爆炸焊接边界效应的力学能量原理[J].上海有色金属, 2003, 24(1):5-11. doi: 10.3969/j.issn.1005-2046.2003.01.002 ZHENG Y M.Mechanics-energy principle for boundary effect in explosion welded material [J].Shanghai Nonferrous Metals, 2003, 24(1):5-11. doi: 10.3969/j.issn.1005-2046.2003.01.002
[3]	朱晓红, 吕新峰, 陈国琦, 等.复合板爆炸焊接的失效分析[J].金属热处理, 2014, 39(1):144-148. http://d.old.wanfangdata.com.cn/Periodical/jsrcl201401038 ZHU X H, LV X F, CHEN G Q, et al.Failure analysis on explosive welded composite plate [J].Heat Treatment of Metals, 2014, 39(1):144-148. http://d.old.wanfangdata.com.cn/Periodical/jsrcl201401038
[4]	邵丙璜, 张凯.爆炸焊接原理及其工程应用[M].大连:大连工学院出版社, 1987. SHAO B H, ZHANG K.Principle and practice of explosive welding [M].Dalian:Dalian University of Technology Press, 1987.
[5]	章冠人, 陈大年.凝聚炸药起爆动力学[M].北京:国防工业出版社, 1991. ZHANG G R, CHEN D N.Condensed explosives detonation dynamics [M].Beijing:National Defense Industry Press, 1991.
[6]	肖定军, 郭学彬, 蒲传金.单孔护壁爆破数值模拟[J].化工矿物与加工, 2008(7):22-24. doi: 10.3969/j.issn.1008-7524.2008.07.007 XIAO D J, GUO X B, PU C J.Numerical simulation for single hole-unilateral blasting [J].Industrial Minerals & Processing, 2008(7):22-24. doi: 10.3969/j.issn.1008-7524.2008.07.007
[7]	LI Y C, SHI D Y, ZHAO Y.ANSYS 11.0/LS-DYNA basic theory and engineering practice [M].Beijing:China Water Power Press, 2008.
[8]	宋锦泉.乳化炸药爆轰特性研究[D].北京: 北京科技大学, 2000. SONG J Q.Research on detonation characteristics of emulsion explosives [D].Beijing: University of Science and Technology Beijing, 2000.
[9]	LIU G R, LIU M B.光滑粒子流体动力学——一种无网格粒子法[M].韩旭, 杨刚, 强洪夫, 译.长沙: 湖南大学出版社, 2005. LIU G R, LIU M B.Smoothed particle hydrodynamics: a meshfree particle method [M].Translated by HAN X, YANG G, QIANG H F.Changsha: Hunan University Press, 2005.
[10]	程国强, 李守新.金属材料在高应变率下的热粘塑性本构模型[J].弹道学报, 2004, 16(4):18-22. doi: 10.3969/j.issn.1004-499X.2004.04.004 CHENG G Q, LI S X.A thermo-viscoplastic constitutive model of metallic materials at high strain rates [J].Journal of Ballistics, 2004, 16(4):18-22. doi: 10.3969/j.issn.1004-499X.2004.04.004
[11]	时党勇, 李裕春, 张胜民.基于ANSYS/LS-DYNA 8.1进行显式动力分析[M].北京:清华大学出版社, 2005. SHI D Y, LI Y C, ZHANG S M.Explicit dynamic analysis based on ANSYS/LS-DYNA 8.1 [M].Beijing:Tsinghua University Press, 2005.
[12]	饶常青.不锈钢/普碳钢厚板坯的爆炸复合[D].南京: 南京理工大学, 2003.