Mechanical and Thermal Dissipation Analysis of Aluminum in Quasi-Isentropic Compression
-
摘要: 为获取高压下材料的纯热力学压力-比容参考线和完全物态方程，减去应力-应变曲线中的其它信息，对准等熵压缩实验中由加载应变率引起的黏性耗散和热传导引起的热耗散做了分析讨论。基于反积分计算和流体动力学积分计算相结合的方法，根据激光加载(约108 s-1)和磁驱动准等熵压缩(约105 s-1)的实验数据，对材料声速、应力-应变曲线、温度和熵增等物理量进行计算，分析了不同应变率与该物理量的关系；还对热传导和SCG本构模型进行了计算，分析了热传导引起的温度变化对材料屈服强度、剪切模量和拉格朗日声速的影响。结果表明：激光加载实验中，应变率引起的温升差异约为180 K, 熵增差异约为250 J/(kg·K)，热传导导致温度下降40 K; 磁驱动准等熵压缩应变率较低，引起的熵增变化小于8 J/(kg·K)。Abstract: To study the pressure-specific volume (p-v) reference line and equation of state from the stress-strain curve of material at high pressure, the viscous dissipation due to loading strain rate and thermal dissipation due to irreversible heat conduction in quasi-isentropic compression experiment (ICE) were discussed and analyzed.A backward integration and forward integration method was used to analyze the data in laser driving and magnetic pressure driving ICE with different strain rates.For viscous dissipation, the sound speed, stress-strain curve, temperature and entropy production during loading were obtained, and the relations between high strain rate and these physical quantities were discussed.For thermal dissipation, through the calculation of the thermal conduction and SCG constitutive model, the variation of temperature and the corresponding yield strength, shear module and sound speed were presented.The results show that:in the laser driving ICE with a high strain rate of 108 s-1), the temperature variation caused by high strain rate is about 180 K, and the entropy production due to heat conduction is about 250 J/(kg·K); and in the magnetic pressure driving with a relatively low strain rate of 105 s-1, the entropy production is less than 8 J/(kg·K).
-
Key words:
- backward integration method /
- viscous force /
- strain rate /
- thermal conduction
-
图 1(b) 计算所得10 μm Al靶中不同位置处的黏性力
Figure 1(b). Calculated viscous stress at 3 different positions of the 10 μm Al target in the laser driving ICE
图 2 激光驱动加载10 μm Al靶实验中，考虑黏性力前、后Al/LiF界面的应力、速度、拉格朗日声速及应力-应变曲线
Figure 2. Profiles of stress, particle velocity, Lagrangian sound speed and stress-strain relation at the Al/LiF interface in the laser driving 10 μm Al ICE with or without viscous force
图 3 20 μm Al靶内不同位置处的计算结果
Figure 3. Calculated results at 4 different Lagrangian positions of the 20 μm Al target in the laser driving ICE
图 4 CQ-4等熵加载1.012 mm Al靶的实验和计算结果
Figure 4. Measured and calculated results of the 1.012 mm Al on CQ-4
图 5(a) 1.012 mm Al靶内不同位置处的应变率-压缩比曲线
Figure 5(a). Strain rate vs. volume compression at different Lagrangian positions of the 1.012 mm Al on CQ-4
图 5(b) 1.012 mm Al靶内不同位置处熵增与冲击熵增的比较
Figure 5(b). Entropy vs. volume compression at different Lagrangian positions of the 1.012 mm Al on CQ-4
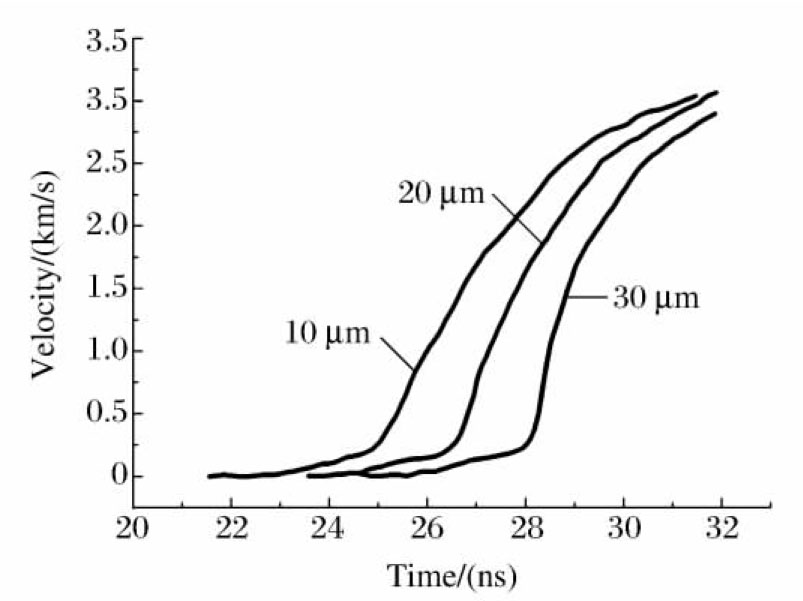
图 6 激光加载实验中考虑热传导后计算所得Al/LiF界面速度与测量结果[5]的对比
Figure 6. Comparison of calculated and measured velocity profiles at the Al/LiF interface in the laser driving ICE
图 7 激光加载实验中考虑热传导前、后，计算所得Al/LiF界面处的温度
Figure 7. Comparison of temperature at the Al/LiF interface with or without heat conduction in the laser driving ICE
图 8 激光加载实验中考虑热传导前、后，计算所得材料的屈服强度
Figure 8. Comparison of yield strength with or without heat conduction in the laser driving ICE
图 9 激光加载实验中考虑热传导前、后，计算所得材料的剪切模量
Figure 9. Comparison of shear modulus with or without heat conduction in the laser driving ICE
图 10 采用不同初始屈服强度的率相关SCG模型计算得到的应力-应变曲线
Figure 10. Stress-strain curve by SCG model with different initial yield strengths
图 11 采用不同初始屈服强度的率相关SCG模型计算得到的拉格朗日声速
Figure 11. Lagrangian sound speed by SCG model with different initial yield strengths
-
[1] Seagle C T, Davis J P, Martin M R, et al. Shock-ramp compression: Ramp compression of shock-melted tin[J]. Appl Phys Lett, 2013, 102(24): 244104. doi: 10.1063/1.4811745 [2] Davis J P. Experimental measurement of the principal isentrope for aluminum 6061-T6 to 240 GPa[J]. J Appl Phys, 2006, 99: 103512. doi: 10.1063/1.2196110 [3] 张红平, 王桂吉, 李牧, 等.准等熵压缩下金属钽的屈服强度分析[J].高压物理学报, 2011, 25(4): 321-326. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gywlxb201104007Zhang H P, Wang G J, Li M, et al. Yield strength analysis of tantalum in quasi-isentropic compression[J]. Chinese Journal of High Pressure Physics, 2011, 25(4): 321-326. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gywlxb201104007 [4] Ding J L, Asay J R. Material characterization with ramp wave experiments[J]. J Appl Phys, 2007, 101(7): 073517. doi: 10.1063/1.2709878 [5] Smith R F, Eggert J H, Jankowski A, et al. Stiff response of aluminum under ultrafast shockless compression to 110 GPa[J]. Phys Rev Lett, 2007, 98(6): 065701. doi: 10.1103/PhysRevLett.98.065701 [6] Davis J P. Charice 1.0: An IDL application for characteristics-based inverse analysis of isentropic compression experiments, SAND 2007-4984[R]. Albuquerque: Sandia National Laboratories, 2007. [7] Wang G J, Zhao J H, Zhang H P, et al. Advances in quasi-isentropic compression experiments at institute of fluid physics of CAEP[J]. Eur Phys J Special Topics, 2012, 206(1): 163-172. doi: 10.1140/epjst/e2012-01597-y [8] Steinberg D J, Lund C M. A constitutive model for strain rates from 10-4 to 106 s-1[J]. J Appl Phys, 1989, 65(4): 1528-1533. doi: 10.1063/1.342968 [9] Steinberg D J. A rate-dependent constitutive model for molybdenum[J]. J Appl Phys, 1993, 74(6): 3827-3831. doi: 10.1063/1.355316 -
下载:
点击查看大图
计量
- 文章访问数: 6633
- HTML全文浏览量: 2074
- PDF下载量: 238
